Suppose the greeks of the value of a derivative security are defined by 

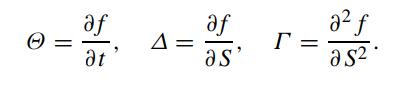
(a) Find the relation between Θ and Γ for a delta-neutral portfolio where Δ = 0. 

(b) Show that the theta may become positive for an in-the-money European call option on a continuous dividend paying asset when the dividend yield is sufficiently high. 

(c) Explain by financial argument why the theta value tends asymptotically to −rXe^−rτ from below when the asset value is sufficiently high.

Transcribed Image Text:

af at af as' Г= a2 f a S2