Let P () denote the European put price normalized by the asset price, that is, We

Let P_α(τ) denote the European put price normalized by the asset price, that is,

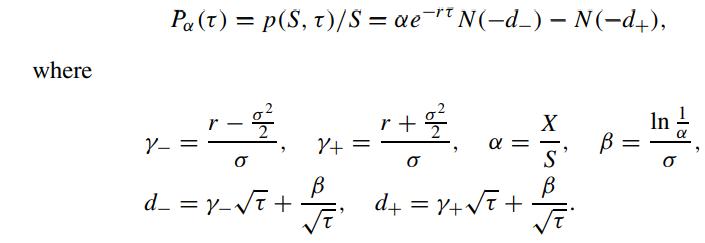We would like to explore the behavior of the temporal rate of change of the European put price. The derivative of P_α(τ) with respect to τ is found to be

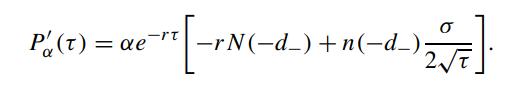
Define f (τ) by the relation P′_α(τ) = αe^−rτ f (τ), and the quadratic polynomial p₂(τ) by

(b) When none of the above conditions (i)–(iii) hold, then P′_α (τ) ≤ 0 for all τ ≥ 0.

Transcribed Image Text:

where Pa (T) = P(S, T)/S=aert N(-d_) — N(-d+), x-=^-²² Y_= σ В d_= = y_ √F + f/₁ Y+ = r+ % σ α d+=y+√7 + X - S В В