To derive the backward FokkerPlanck equation, we consider where u is some intermediate time satisfying t 0
Question:
To derive the backward Fokker–Planck equation, we consider
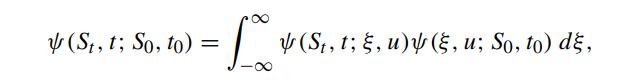
where u is some intermediate time satisfying t0
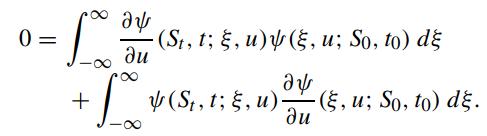 From the forward Fokker–Planck equation derived in Problem 3.8, we obtain.
From the forward Fokker–Planck equation derived in Problem 3.8, we obtain.
![you ave - (St, t; &, u) (, u; So, to) de - Led- SE + -[(, u)(, u; So, to)] 2 (, u) [6-8, 4:50.40]] (5.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/4/6/8/539655b173b836a01700468538626.jpg)
Problem 3.8
Let the dynamics of the stochastic state variable St be governed by the Ito process
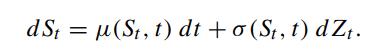
For a twice differentiable function f (St), the differential of f (St) is given by
![af (St, t) f df = [u(S. 1) 25 + 0 (5, 1) 8/17] a St 2 as? ]dt +0 af dt + o (St, t) dZt. a St](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/4/6/8/319655b165f6e93b1700468318535.jpg)

Perform parts integration of the integral in (ii).
By performing parts integration of the last integral and taking the limit u → t0, show that ψ(St,t; S0,t0) satisfies
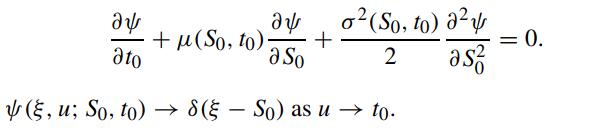
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





