Use (4.2.21) to derive the following partial differential equation for the floating strike lookback put option 

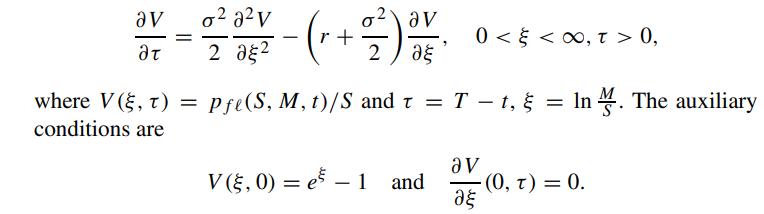
Solve the above Neumann boundary value problem and check the result with the put price formula given in (4.2.10). 

Define W = ∂V/∂ξ so that W satisfies the same governing differential equation but the boundary condition becomes W(0,τ) = 0. Solve for W(ξ,τ), then integrate W with respect to ξ to obtain V . Be aware that an arbitrary function ∅(t) is generated upon integration with respect to ξ . Obtain an ordinary differential equation for ∅(t) by substituting the solution for V into the original differential equation.

Transcribed Image Text:

av ат = 0² 3² 2 agt - (r+²²³) ar 2 ὃξ 0 < <∞, T > 0, where V (s, t) = Pfe(S, M, t)/S and t = T - t, & = ln . The auxiliary conditions are V (,0) = e 1 and - av a (0, T) = 0.