We would like to compute d(S T X) + , where S t follows the Geometric Brownian

Question:

We would like to compute d(S_T −X)⁺, where S_t follows the Geometric Brownian process

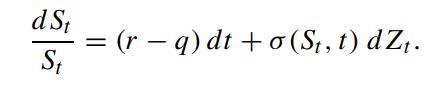d St St = = (r - q) dt+o (St, t) dZt. The function (S_T − X)⁺ has a discontinuity at S_T = X. Rossi (2002) proposed to approximate (S_T − X)⁺ by the following function f (S_T) whose first derivative is continuous, where

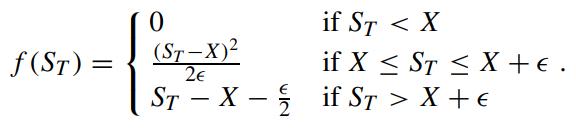
f(ST) = 0 (ST-X) 2 ST-X- 2 if ST < X if X ST < X+. if ST if ST X +

Here, є is a small positive quantity. By applying Ito’s lemma, show that

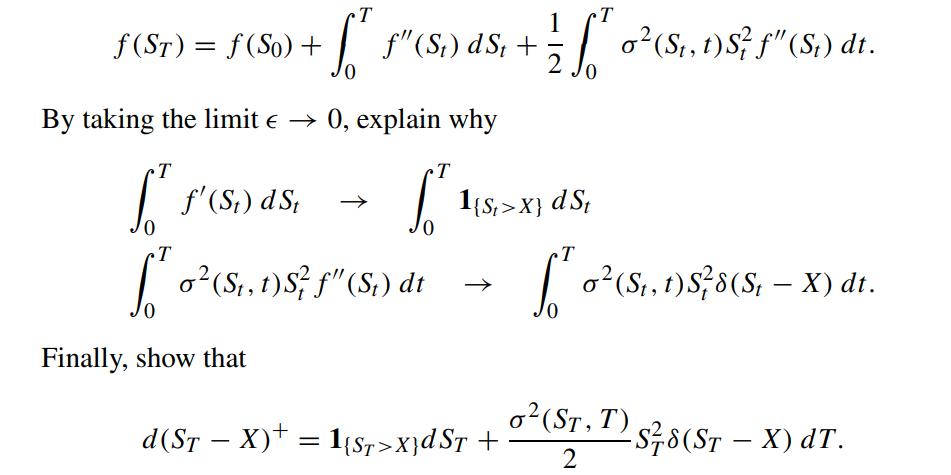
f(ST) = f(So) + T T 1 fo f" (St) dSt + 5 + 2/2 o (St, t)s f" (S) dt. - 0 By taking the limit 0, explain

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Mathematical Models Of Financial Derivative

ISBN: 9783642447938

2nd Edition

Authors: Yue-Kuen Kwok

See More Books

Question Posted: Dec 02, 2023 03:57 AM

See More Questions

Evaluate the integral in terms of the constants. L x x dx = 0 if n is an odd whole number. Explain graphically. Use FTC I to show that
For the functions f(x)=2-x and g(x)=x+2x-48, find f+g, f-g, fg, and Determine the domain for each function. g (f+g)(x)=(Simplify your answer.)
The following letter has errors in spelling, proofreading, verbs, sentence structure, parallelism, and other writing techniques studied in this chapter. You may either (a) Use standard proofreading...
In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hos & S.D of bohos Estimate the ne of likely to burn for it...
Assume the Federal Interstate Commission began the fiscal year with the following account balances: 1. Congress passed a spending bill providing $12,000,000 to fund the agencys operations for the...
Suppose a firm makes purchases of $3.65 million per year under terms of 2/10, net 30, and takes discounts. a. What is the average amount of accounts payable net of discounts? (Assume the $3.65...
A company reports net income of $75,000. Its weightedaverage common shares outstanding is 19,000. It has no other stock outstanding. Its earnings per share is: a. $4.69 b. $3.95 c. $3.75 d. $2.08 e....
The values of outstanding bonds change whenever the going rate of interest changes. In general, short-term interest rates are more volatile than long-term interest rates. Therefore, short-term bond...
a. 17.86 years b. 20.16 years c. 19.06 years d. 12.72 years e. 15.16 years
By applying the following transformation on the dependent variable in the BlackScholes equation while the auxiliary conditions are transformed to become Consider the following diffusion equation...
Assume that the time dependent volatility function (t) is deterministic. Suppose we write imp (t, T) as the implied volatility obtained from the time-t price of a European option with maturity T ,...
Compute (a) The characteristic polynomial of A, (b) The eigenvalues of A, (c) A basis for each eigenspace of A, (d) The algebraic and geometric multiplicity of each eigenvalue. 2 1 1 1 A = L0 0 0 2...
Q Proprietorinc (the lessee) enters into a 10 year lease of a property with an option to extend the contract for 5 years. Lease payments are $50,000 per year, payable at the beginning of each year....
1.Think about your investment Possibility for 3 years holding period in real investment environment? A.What could be your investment objectives? B. What amount of fund you could invest for three...
3- The student council normally sells 1500 school T-shirts for $12 each. This year they plan to decrease the price of the T-shirts. Based on student feedback, they know that for every $0.50 decrease...
2. The notation {f(x): x S} means "the set of all values that can be produced by substituting an element x of set S into f(x)." For example, the set of all odd integers can be expressed as {2k+1kZ}....
Implementation guidance for IFRS 2 indicates that it "accompanies, but is not part of, IFRS 2." In other words, this implementation guidance is considered mandatory. integral to the standard. not...
In Problem 1-4, use the fact that To find the limits? 1. 2. 3. 4. lim f(x) = lim f( rt im + IT lim( 1 + 1T lim 1+
The Cholesterol Level data sets give cholesterol levels of heart attack patients. Cholesterol measures are taken 2, 4, and 14 days aft er a patient has suffered a heart attack. Is there a significant...
Are seasonal discounts appropriate in agricultural businesses (which are certainly seasonal)?
What are the effective annual interest rates for the following cash discount terms: ( a ) 1/10, net 20; ( b ) 1/5, net 10; and ( c ) net 25?
Why would a manufacturer offer a rebate instead of lowering the suggested list price?
Sociology
I am unsure how to answer question e as there are two variable changes. In each of the following, you are given two options with selected parameters. In each case, assume the risk-free rate is 6% and...
On January 1, Interworks paid a contractor to construct a new cell tower at a cost of $850,000. The tower had an estimated useful life of ten years and a salvage value of $100,000. Interworks...

We would like to compute d(S T X) + , where S t follows the Geometric Brownian

Question:

d St St = = (r - q) dt + o (St, t) dZt.

Step by Step Answer:

The problem involves mathematical derivations and limits using stochastic calculus concepts like ...View the full answer

Mathematical Models Of Financial Derivative

Students also viewed these Business questions