Assume that the time dependent volatility function (t) is deterministic. Suppose we write imp (t, T)
Question:
Assume that the time dependent volatility function σ(t) is deterministic. Suppose we write σimp (t, T) as the implied volatility obtained from the time-t price of a European option with maturity T , for T > t. Show that
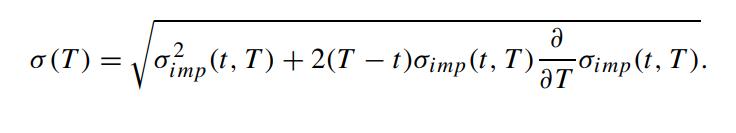
In real situations, we may have the implied volatility available only at discrete times Ti,i = 1, 2, ··· ,N. Assuming the volatility σ(T) to be piecewise constant over each time interval [Ti−1,Ti],i = 1, 2, ··· ,N, show that
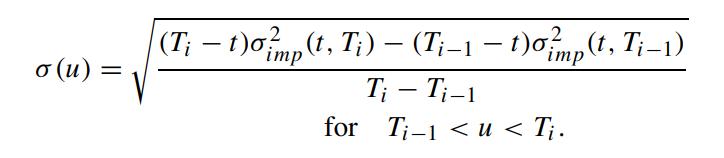 The implied volatility σimp(t, T ) and the time dependent volatility function σ(t) are related by
The implied volatility σimp(t, T ) and the time dependent volatility function σ(t) are related by
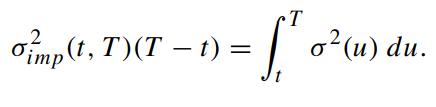
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





