New Semester
Started
Get
50% OFF
Study Help!
--h --m --s
Claim Now
Question Answers
Textbooks
Find textbooks, questions and answers
Oops, something went wrong!
Change your search query and then try again
S
Books
FREE
Study Help
Expert Questions
Accounting
General Management
Mathematics
Finance
Organizational Behaviour
Law
Physics
Operating System
Management Leadership
Sociology
Programming
Marketing
Database
Computer Network
Economics
Textbooks Solutions
Accounting
Managerial Accounting
Management Leadership
Cost Accounting
Statistics
Business Law
Corporate Finance
Finance
Economics
Auditing
Tutors
Online Tutors
Find a Tutor
Hire a Tutor
Become a Tutor
AI Tutor
AI Study Planner
NEW
Sell Books
Search
Search
Sign In
Register
study help
mathematics
applied calculus
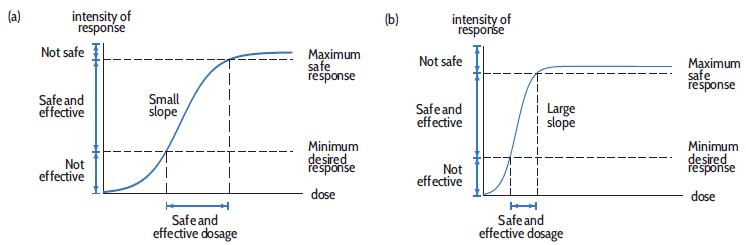
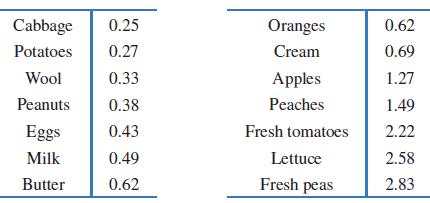
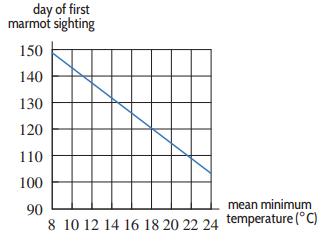
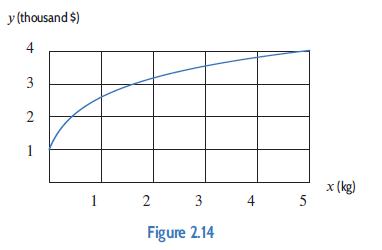
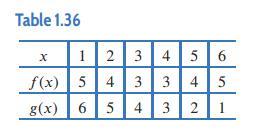
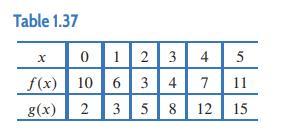
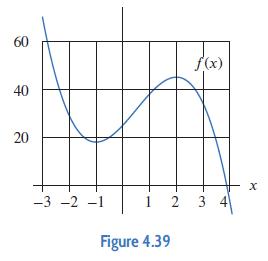
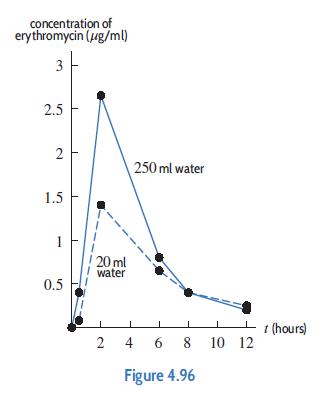
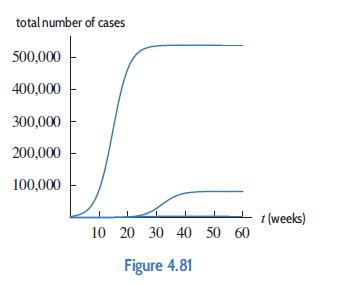
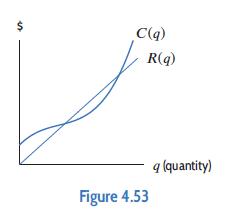
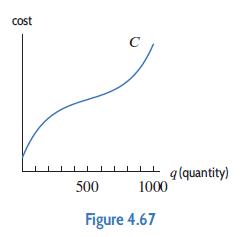
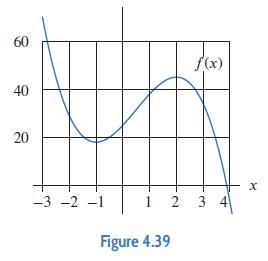
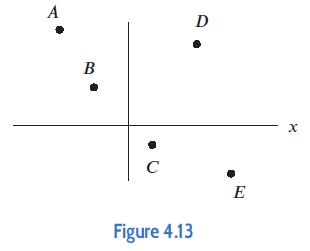
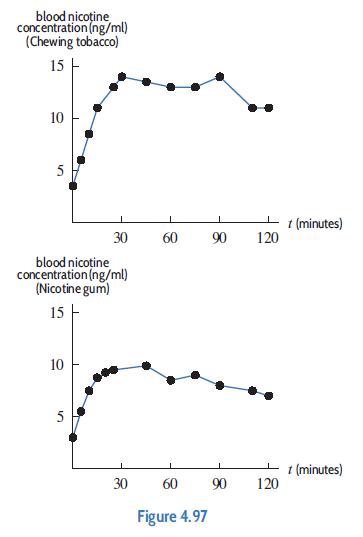
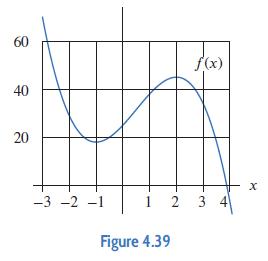
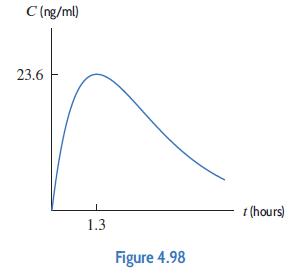
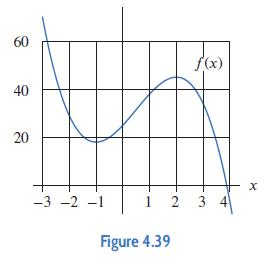
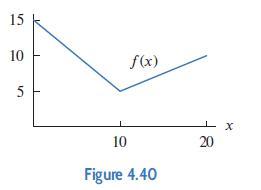
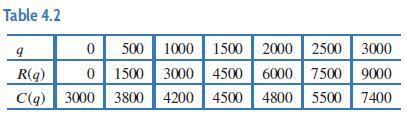
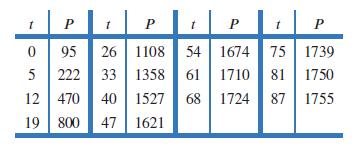
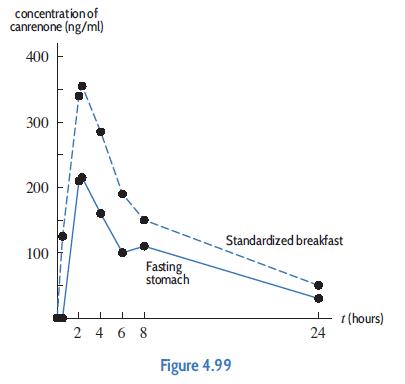
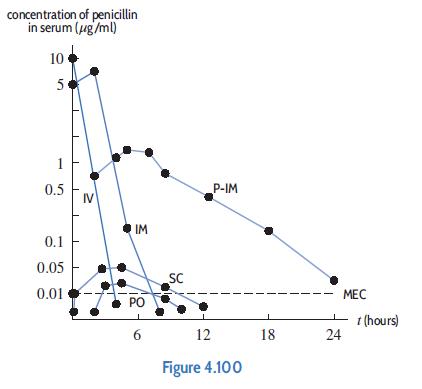
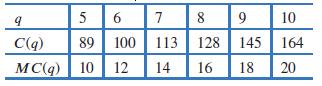
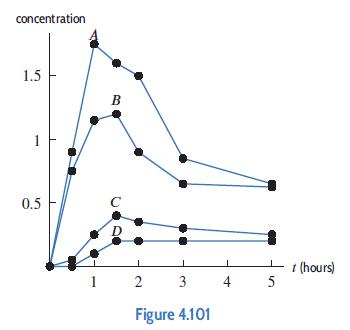
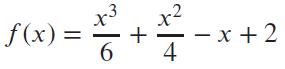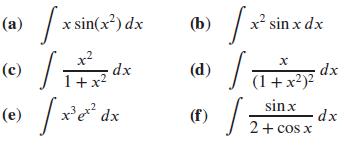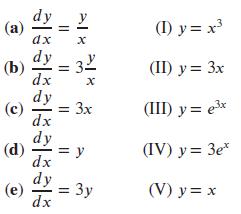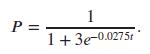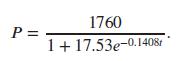Applied Calculus 6th Edition Deborah Hughes Hallett, Patti Frazer Lock, Andrew M. Gleason, Daniel E. Flath, Sheldon P. Gordon, David O. Lomen, David Lovelock, William G. McCallum, Brad G. Osgood, Andrew Pasquale - Solutions
Differentiate the functions in Problems. Assume that A, B, and C are constants.P(t) = Cet.
Find the derivative of the functions in Problems.f(x) = (ln x)3
Find the derivative. Assume a, b, c, k are constants. y = 1 77/2
Differentiate the functions in Problems. Assume that A and B are constants. f(0) = sin 0 0
Find the derivative. Assume that a, b, c, and k are constants.f(w) = (5w2 + 3)ew2
Differentiate the functions in Problems. Assume that A, B, and C are constants.y = B + Aet
Find the derivative of the functions in Problems.f(x) = ln(ln x)
For Problems find the derivative. Assume a, b, c, k are constants.y = √x
Find the derivative. Assume that a, b, c, and k are constants.y = x ⋅ 2x
Differentiate the functions in Problems. Assume that A and B are constants.f(θ) = θ3 cos θ
Differentiate the functions in Problems. Assume that A, B, and C are constants.P(t) = 3000(1.02)t
Find the derivative. Assume that a, b, c, and k are constants. y= et 1 + ex
The average adult takes about 12 breaths per minute. As a patient inhales, the volume of air in the lung increases. As the patient exhales, the volume of air in the lung decreases. For t in seconds since start of the breathing cycle, the volume of air inhaled or exhaled since t = 0 is given, in
Differentiate the functions in Problems. Assume that A, B, and C are constants.y = t2 + 5 ln t
Find the derivative of the functions in Problems.f(θ) = (eθ + e−θ)−1
Find the derivative. Assume a, b, c, k are constants. 7 y = 315-5√t +- t
Find the derivative. Assume that a, b, c, and k are constants. w = 3y + y² 5+y
If t is the number of months since June, the number of bird species, N, found in an Ohio forest oscillates approximately according to the formula(a) Graph f(t) for 0 ≤ t ≤ 24 and describe what it shows. Use the graph to decide whether f'(1) and f'(10) are positive or negative.(b) Find f'(t).(c)
Differentiate the functions in Problems. Assume that A, B, and C are constants.R(q) = q2 − 2 ln q
Find the derivative. Assume a, b, c, k are constants. h(0) = 1 ' Ꮎ
Find the equation of the tangent line to the graph of y = sin x at x = π. Graph the function and the tangent line on the same axes.
Differentiate the functions in Problems. Assume that A, B, and C are constants.y = 10x + 10/x
Find the derivative of the functions in Problems.y = 5 + ln(3t + 2)
Find and interpret the value of the expression in practical terms. Let C(t) be the concentration of carbon dioxide in parts per million (ppm) in the air as a function of time, t, in months since December 1, 2005:C'(60) C(t) = 3.5 sin (%) + : +381 + 등
Differentiate the functions in Problems. Assume that A, B, and C are constants.y = x2 + 4x − 3 ln x
Find the derivative. Assume a, b, c, k are constants. 12 y = 3t² + √t | 1 12
Find the relative rate of change f¨(t)∕f(t) at the given value of t. Assume t is in years and give your answer as a percent.f(t) = 2e0.3t; t = 7
Find the derivative. Assume that a, b, c, and k are constants. f(x) = ax + b cx + k
Find and interpret the value of the expression in practical terms. Let C(t) be the concentration of carbon dioxide in parts per million (ppm) in the air as a function of time, t, in months since December 1, 2005:C'(36) C(t) = 3.5 sin (%) + : +381 + 등
Differentiate the functions in Problems. Assume that A, B, and C are constants.f(t) = Aet + B ln t
Find the derivative of the functions in Problems. f(x) = √√2+√x
Find the derivative. Assume a, b, c, k are constants. h(t) = + 3 t 4 12
Find the derivative of the functions in Problems.P = (1 + ln x)0.5
Find the derivative. Assume a, b, c, k are constants. y = z² - IN 1 2z
Find the derivative. Assume that a, b, c, and k are constants. w = 3z 1 + 2z
Is the graph of y = sin(x4) increasing or decreasing when x = 10? Is it concave up or concave down?
Differentiate the functions in Problems. Assume that A, B, and C are constants.R = 3 ln q
Find the derivative of the functions in Problems.y = √ex + 1
Find the derivative. Assume a, b, c, k are constants.R = (s2 + 1)2
Find the derivative. Assume that a, b, c, and k are constants. Z= 1+1
Find the equations of the tangent lines to the graph of f(x) = sin x at x = 0 and at x = π∕3. Use each tangent line to approximate sin(π∕6). Would you expect these results to be equally accurate, since they are taken equally far away from x = π∕6 but on opposite sides? If the accuracy is
Differentiate the functions in Problems. Assume that A, B, and C are constants.D = 10 − ln p
Find the derivative of the functions in Problems.y = 5x + ln(x + 2)
For Problems find the derivative. Assume a, b, c, k are constants.z = (t − 1)(t + 1)
Find the derivative. Assume that a, b, c, and k are constants. f(x) = X er
Find the line tangent to f(x) = 3x + cos(5x) at the point where x = 0.
Differentiate the functions in Problems. Assume that A, B, and C are constants.f(x) = Aex − Bx2 + C
Find the derivative of the functions in Problems.y = (5 + ex)2
Find the derivative. Assume that a, b, c, and k are constants.z = (te3t + e5t)9
Find the integrals in Problem. Z e² dz
Find the integrals in Problem. Check your answers by differentiation. (5x-7)¹⁰ dx
Use the Fundamental Theorem to evaluate the definite integral exactly. √ 2 (6q² + 4) dq
Figure 6.5 shows f. If F' = f and F(0) = 0, find F(b) for b = 1, 2, 3, 4, 5, 6. -1 f(1) 2 3 Figure 6.5 -4 5 10 1
Find the integrals in Problem. y 05-y dy
Sketch possible supply and demand curves where the consumer surplus at the equilibrium price is(a) Greater than the producer surplus.(b) Less than the producer surplus.
Which of (I)–(V) are antiderivatives off(x) = 2 sin x cos x?I. −2 sin x cos xII. 2 cos2 x − 2 sin2xIII. sin2xIV. −cos2 xV. 2 sin2x + cos2 x
(a) Find the present and future value of an income stream of $6000 per year for a period of 10 years if the interest rate, compounded continuously, is 5%.(b) How much of the future value is from the income stream? How much is from interest?
Find the integrals in Problems. / (1+2)√/2+31 dt
A person deposits money into an account, which pays 6% interest compounded continuously, at a rate of $1000 per year for 30 years. Calculate:(a) The balance in the account at the end of the 30 years.(b) The amount of money actually deposited into the account.(c) The interest earned during the 30
(a) Using Figure 6.4, estimate ∫70 f(x)dx.(b) If F is an antiderivative of the same function f and F(0) = 25, estimate F(7). 42 2 -2 -4 -6 -8 Figure 6.4 f(x) x
For a product, the demand curve is p = 100e−0.008q and the supply curve is p = 4√q + 10 for 0 ≤ q ≤ 500, where q is quantity and p is price in dollars per unit.(a) At a price of $50, what quantity are consumers willing to buy and what quantity are producers willing to supply? Will the
Use the Fundamental Theorem to evaluate the definite integral exactly. J =dx x
Find the integrals in Problem. Check your answers by differentiation. 1² x sin(x²)dx
(a) An investment account earns 10% interest compounded continuously. At what constant, continuous rate must a parent deposit money into such an account in order to save $100,000 in 10 years for a child’s college expenses?(b) If the parent decides instead to deposit a lump sum now in order to
Decide whether the expression is a number or a family of functions. (Assume f(x) is a function.) +²) dx x
Supply and demand data are in Tables 6.3 and 6.4.(a) Which table shows supply and which shows demand?(b) Estimate the equilibrium price and quantity.(c) Estimate the consumer and producer surplus. Table 6.3 q (quantity) p (S/unit) 60 50 50 Table 6.4 0 100 200 300 400 500 q (quantity) p
Find the integrals in Problem. - √x lnx dx
Find the integrals in Problem. Check your answers by differentiation. [P(P = 3)¹⁰ di 1² (1³ dt
Use the Fundamental Theorem to evaluate the definite integral exactly. T (x³ - лx²) dx 2
In Problem sketch two functions F such that F' = f. In one case let F(0) = 0 and in the other, let F(0) = 1. -1 - f(x) X
The total gains from trade (consumer surplus + producer surplus) is largest at the equilibrium price. What about the consumer surplus and producer surplus separately?(a) Suppose a price is artificially high. Can the consumer surplus at the artificial price be larger than the consumer surplus at the
Decide whether the expression is a number or a family of functions. (Assume f(x) is a function.) [ - [ f(x) dx f(x) dx +
Find the integrals in Problem. [XVI-ydy
Use the Fundamental Theorem to evaluate the definite integral exactly. 1 2 1 xp =
Decide if the function is an antiderivative of f(x) = 2e2x. + S' F(x) = ²x + e²¹ dt
Find the integrals in Problem. Check your answers by differentiation. [ 2x(x² + 1)³dx
Find the integrals in Problems. [y√y+3dy
Let F(x) be an antiderivative of f(x), with F(1) = 20 and ∫41 f(x) dx = −7. What is F(4)?
Find the integrals in Problem. q³ In 5q dq
Use the Fundamental Theorem to evaluate the definite integral exactly. (3 (31² +41 +3) dt
Assuming an interest rate of 5% compounded continuously,(a) Find the future value in 6 years of a payment of $12,000 made today.(b) Find the future value of an income stream of $2000 per year over 6 years.(c) Which is larger, the future value from the lump sum in part (a) or from the income stream
Explain how you can tell if substitution can be used to find an antiderivative. [s sint cost dt
Use the Fundamental Theorem to evaluate the definite integral exactly. (12 (12x² + 1) dx
The demand and supply curves for a product are given as2q − 15p = −1203q + 6p = 105.(a) Find the consumer surplus at the equilibrium.(b) Find the producer surplus at the equilibrium.
Explain how you can tell if substitution can be used to find an antiderivative. 1: x Inx dx
Let F(x) be an antiderivative of f(x), with F(0) = 50 and ∫50 f(x) dx = 12. What is F(5)?
Assuming an interest rate of 3% compounded continuously,(a) Find the future value in 10 years of a payment of $10,000 made today.(b) Find the future value of an income stream of $1000 per year over 10 years.(c) Which is larger, the future value from the lump sum in part (a) or from the income
Find the integrals in Problems. J (z+1)e²² dz
Decide if the function is an antiderivative of f(x) = 2e2x.F(x) = 2e2x
Find the consumer surplus for the demand curve p = 100 − 4q when q∗ = 10 items are sold at the equilibrium price.
Find the integrals in Problems. y ln ydy
If G(1) = 50 and G(x) is an antiderivative of g(x) = ln x, use a calculator to find G(4).
Explain how you can tell if substitution can be used to find an antiderivative. In x X dx
(a) Find the present and future value of an income stream of $5000 per year for a period of 8 years if the interest rate, compounded continuously, is 2%.(b) Explain, in plain language, what the present and future values mean in terms of the income stream.
Explain how you can tell if substitution can be used to find an antiderivative. x(1 - 5x²)5 dx
Decide if the function is an antiderivative of f(x) = 2e2x.F(x) = xe2x
Given the demand curve p = 35 − q2 and the supply curve p = 3 + q2, find the producer surplus when the market is in equilibrium.
Find the integrals in Problems. pe pe-0.1p dp
If F(0) = 5 and F(x) is an antiderivative of f(x) = 3e−x2, use a calculator to find F(2).
Use the Fundamental Theorem to evaluate the definite integral exactly. 3 5 dx
Showing 500 - 600
of 5529
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Last
Step by Step Answers
Get 50% OFF
Claim Now
