Consider the following macroeconomic model:
Y = C + I* + G* + X* − M* (equilibrium of national income)
C = aY_d + b (consumption; 0 < a < 1; b > 0)
T = tY (taxation; 0 < t < 1)
where I*, G*, X*, M* and Yd denote investment, government expenditure, exports, imports and disposable income, respectively.

(a) Show that this system can be expressed as Ax = b where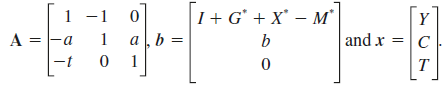

(b) Show that the determinant of A is 1 − a(1 − t)
(c) By using Cramer’s rule, or otherwise, show that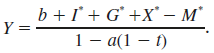

(d) Write down the autonomous investment multiplier for Y and deduce that the change in national income exceeds any increase in investment.
(e) Work out the marginal propensity to consume multiplier for Y and hence state the direction of change in Y due to an increase in a.

Transcribed Image Text:

I+ G' + X' – M 1-1 A =-a and x =| C a, b = -t b + Ỉ + G° +X ° – M° Y =. 1- a(1 – t)