If m = n, then property 1 in Theorem 1 implies that a n a n =
Question:
If m = –n, then property 1 in Theorem 1 implies that a–nan = a0 = 1. Explain how this helps motivate the definition of a–n.
Data from Theorem 1
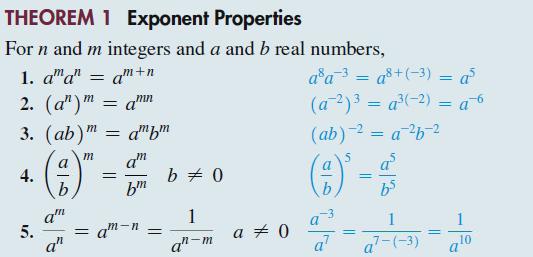
Transcribed Image Text:
THEOREM 1 Exponent Properties For n and m integers and a and b real numbers, 1. ama" = am+n 2. (an) m = amn m 3. (ab) = ambm 4. m = am b b am 5. = am-n = q" b = 0 an-m a = 0 a³ a3 = a8+(-3) = a (a ²)² = a³(-2) = a6 (ab) ² = a ²6-² (3)³ = a² = a² 65 1 a²-(-3) = 10
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 80% (5 reviews)
Detailed Explanation In the expression a n where mn property 5 in theorem 1 states that a mn 1a nm I...View the full answer

Answered By

Branice Buyengo Ajevi
I have been teaching for the last 5 years which has strengthened my interaction with students of different level.
4.30+
1+ Reviews
10+ Question Solved
Related Book For 

Finite Mathematics For Business Economics Life Sciences And Social Sciences
ISBN: 9780134862620
14th Edition
Authors: Raymond Barnett, Michael Ziegler, Karl Byleen, Christopher Stocker
Question Posted:
Students also viewed these Mathematics questions
-
If n = 0, then property 1 in Theorem 1 implies that a m a 0 = a m + 0 = am. Explain how this helps motivate the definition of a 0 . Data from Theorem 1 THEOREM 1 Exponent Properties For n and m...
-
Choose one (1) IT company that you would like to work for and choose one (1) type of product or service that they offer in IT field of expertise. Using the research skills you garnered in your...
-
In this exercise, we consider some policy issues related to public support for schoolsand the coalitions between income groups that might form to determine the political equilibrium. A: Throughout,...
-
Sodium sulfate, Na2SO4 with a mass of 15 g is dissolved in 250 g water. What is the boiling point of the solution? Kb for water = 0.52 C/m a) 100 C b) 100.2 C c) 99.67 C d) 101.2 C c) d) O a) b)
-
A heavy, uniform cylinder has a mass m and a radius R (Figure). It is accelerated by a force T, which is applied through a rope wound around a light drum of radius r that is attached to the cylinder....
-
Show that in Example 2 the y-axis is mapped onto the unit circle in the w-plane.
-
Calculate and interpret residuals.
-
Rossin's Racers has total credit sales for the year of $280,000 and estimates that 3% of its credit sales will be uncollectible. Record the end-of-period adjusting entry on December 31, in general...
-
Pfizer (US company) sells a drug in Canada. Sales: CAD 45.0m Variable Costs: USD 10.0m, Euro 1.5m and CAD 2.0m Current exchange rate: CAD 1.25/USD and USD 1.1/Euro. Calculate the gross margin in USD:...
-
Rainmaker Environmental Consultants is just finishing its second year of operations. The companys unadjusted trial balance at October 31, 2023, follows. Rainmaker prepares adjustments each October...
-
Refer to Problem 51. What is the difference between 2 (3)2 and (2 3 ) 2? Which agrees with the value of 2 3 2 obtained with a calculator? Data from Problem 51 What is the result of entering 2 32 on a...
-
In Problem factor, if possible, as the product of two first degree polynomials with integer coefficients. Use the quadratic formula and the factor theorem 4x 2 + 241x 434
-
Discuss the pros and cons of long-term-care insurance. Does it make sense for anyone in your family right now? Why or why not? What factors might change this assessment in the future?
-
You are the cost accountant of an engineering concern which has three departments - preparation, machining and assembly. The budgeted direct labour hours for the workshops are 8,000, 12,000 and...
-
What alternative to fostering fun and enjoyment at work do you think might have worked for Zappos?
-
Using the techniques of dimensional analysis, and assuming that experimentation shows the dimensionless number to be 1, derive the following equation: E v = Job card two The results of an ultrasonic...
-
Given the historical cost of product Carla Vista is $13, the selling price of product Carla Vista is $15, costs to sell product Carla Vista are $3, the replacement cost for product Carla Vista is...
-
What causes of outliers in statistics and when I create a boxplot why do I not see the outliers. What steps are to take in creating a boxplot?
-
What is a cluster entity type?
-
You are standing on the top of a building and throw a ball vertically upward. After 2 seconds, the ball passes you on the way down, and 2 seconds after that, it hits the ground below. a. What is the...
-
Given the probability density function f(x) = 0.01 3 x 2 e 0.01x / (3), determine the mean and variance of the distribution.
-
Patients arrive at a hospital emergency department according to a Poisson process with a mean of 6.5 per hour. (a) What is the mean time until the 10th arrival? (b) What is the probability that more...
-
The total service time of a multi step manufacturing operation has a gamma distribution with mean 18 minutes and standard deviation 6. (a) Determine the parameters and r of the distribution. (b)...
-
Current Portion of Long-Term Debt PepsiCo, Inc., reported the following information about its long-term debt in the notes to a recent financial statement (in millions): Long-term debt is composed of...
-
Show transcribed image text 31/12/2016 GHS'000 25,500 The following information relates to the draft financial statements of Samanpa Ltd. Summarised statement of financial position as at: 31/12/2017...
-
\ How do i solve this? Beginning raw materials inventory Ending raw materials inventory Direct labor Operating expenses Purchases of direct materials Beginning work in process inventory Ending work...

Study smarter with the SolutionInn App


