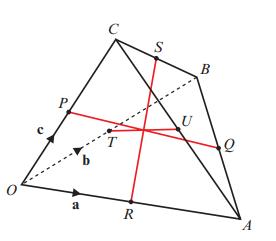
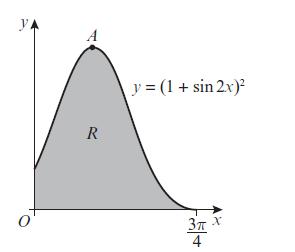
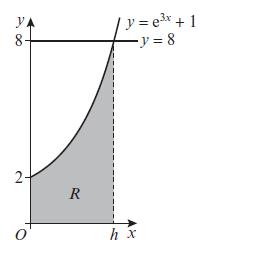
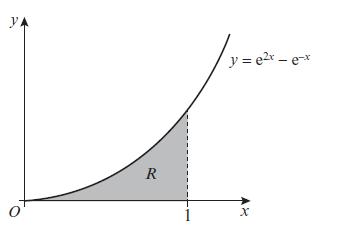
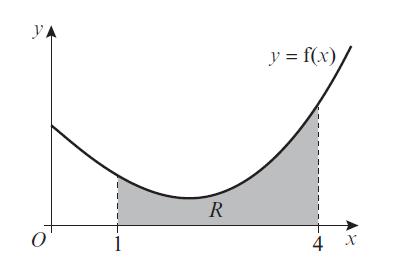
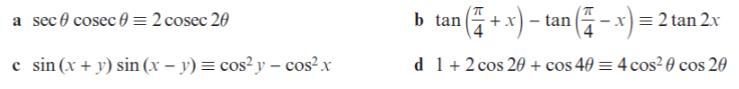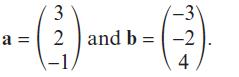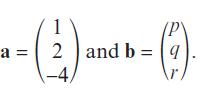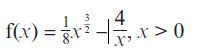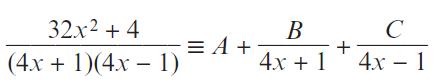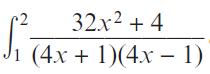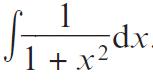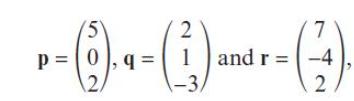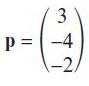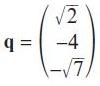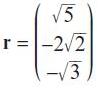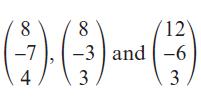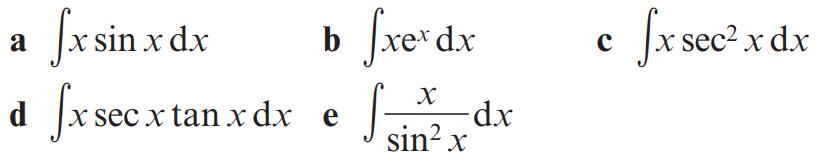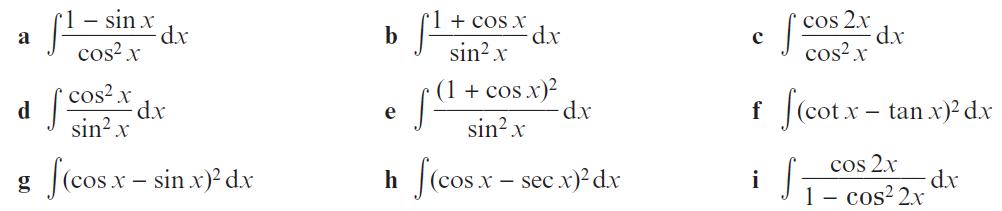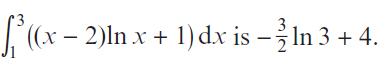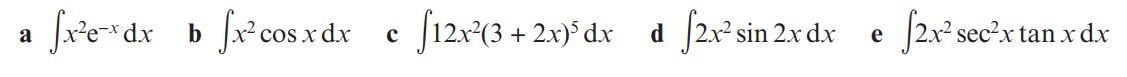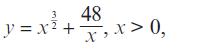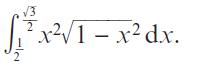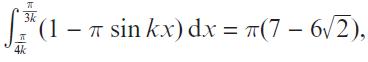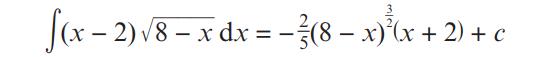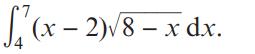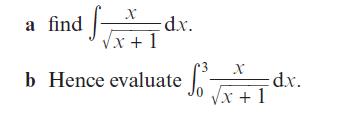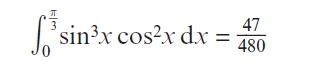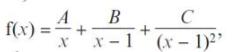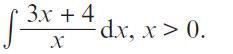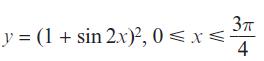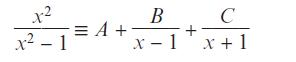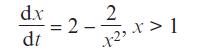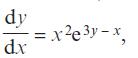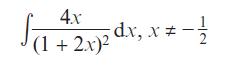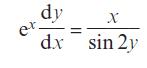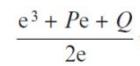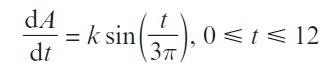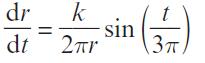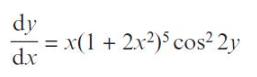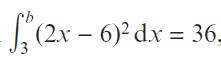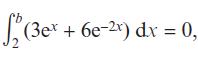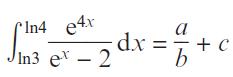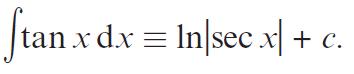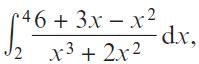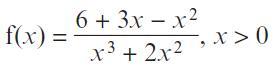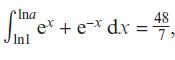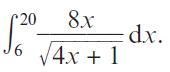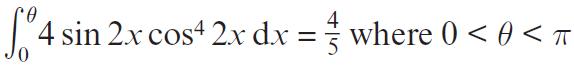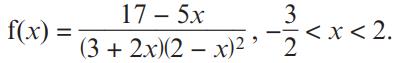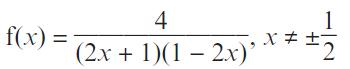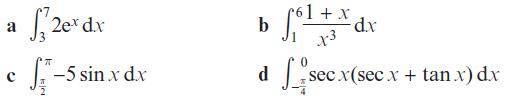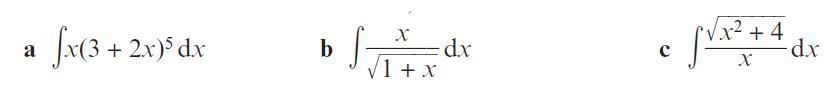Pearson Edexcel A Level Mathematics Pure Mathematics Year 2 1st Edition Greg Attwood, Jack Barraclough, Ian Bettison, David Goldberg, Alistair Macpherson, Joe Petran - Solutions

Unlock the full potential of your understanding with our comprehensive solutions for "Pearson Edexcel A Level Mathematics Pure Mathematics Year 2 1st Edition" by Greg Attwood and colleagues. Dive into online answers key and explore detailed chapter solutions in our solution manual. Access step-by-step answers and solved problems that illuminate the intricacies of mathematics. Our textbook's questions and answers, combined with a robust test bank, offer a thorough learning experience. The instructor manual and solutions PDF ensure clarity and insight, available for free download. Enhance your math skills with our expertly crafted resources.