A collection of N harmonic oscillators at thermal equilibrium at absolute temperature Tis shown by statistical mechanics
Question:
A collection of N harmonic oscillators at thermal equilibrium at absolute temperature Tis shown by statistical mechanics to have the thermodynamic energy
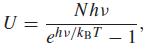
where kB is Boltzmann’s constant, h is Planck’s constant, T is the absolute temperature, and ν is the vibrational frequency. Find the limit of U as ν → 0. Find the limit of U as T → 0.
As ν → 0, both the numerator and denominator approach zero. We apply l’Hôpital’s rule. The derivative of the numerator with respect to ν is equal to Nh. The derivative of the denominator is
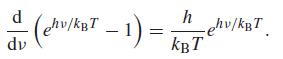
As ν → 0, this derivative approaches h/kBT.
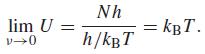
As T → 0 there is no need to apply l’Hôpital’s rule. The numerator remains constant, but the denominator becomes large without bound so that
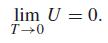
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





