If AÌ‚ is the operator corresponding to the mechanical
quantity A and Ï•_nis an eigenfunction of AÌ‚, such that

Âϕ_n = a_nϕ_n

show that the expectation value of A is equal to a_n if the state of the system corresponds to Ï•_n. See Problem 5 for the formula for the expectation value.

Problem 5

In quantum mechanics, the expectation value of a mechanical quantity is given by

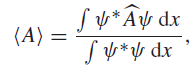
where  is the operator for the mechanical quantity and ψ is the wave function for the state of the system. The integrals are over all permitted values of the coordinates of the system. The expectation value is defined as the prediction of the mean of a large number of measurements of the mechanical quantity, given that the system is in the state corresponding to ψ prior to each measurement.

For a particle moving in the x direction only and confined to a region on the x axis from x = 0 to x = a, the integrals are single integrals from 0 to a and pÌ‚_x is given by („/i)ˆ‚/ˆ‚x. The wave normalized function is

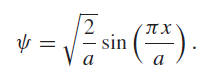
Normalization means that the integral in the denominator of the expectation value expression is equal to unity.

SV* dx (A) = S* dx sin a a