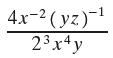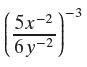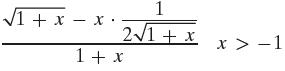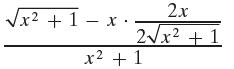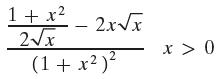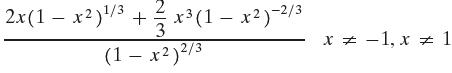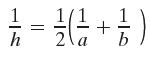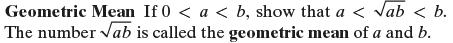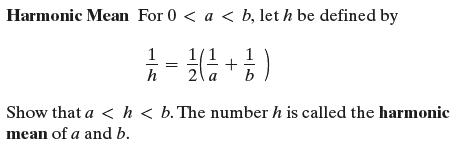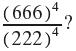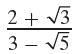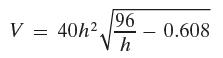Precalculus Concepts Through Functions A Unit Circle Approach To Trigonometry 5th Edition Michael Sullivan - Solutions
Unlock the full potential of your mathematical journey with our comprehensive resource for "Precalculus Concepts Through Functions: A Unit Circle Approach to Trigonometry, 5th Edition" by Michael Sullivan. Access online solutions, answers key, and a detailed solution manual that provide step-by-step answers to all textbook problems. Explore solved problems and test bank questions, along with chapter solutions available in solutions PDF format. Enhance your understanding with our instructor manual designed to complement your learning. Discover the convenience of questions and answers, all available for free download, aiding students in mastering precalculus concepts effectively.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()