Extracted communalities and eigenvalues can be computed from an unrotated factor matrix. An extracted eigenvalue is the
Question:
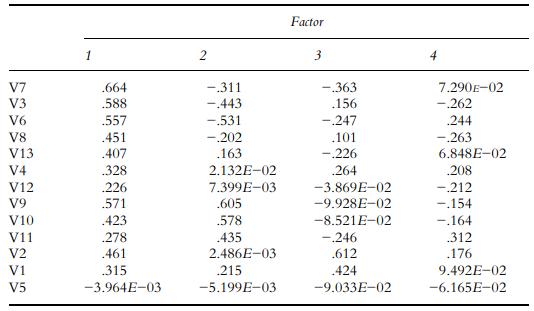
Extracted communalities and eigenvalues can be computed from an unrotated factor matrix. An extracted eigenvalue is the sum of the squared loadings of the items on a factor. An extracted communality is the sum of the squared loadings for a variable across all factors. Table 18.2 is the unrotated factor matrix from the analysis requested. Extraction Method: Principal Axis Factoring 4 factors extracted, 20 iterations required
Using information presented in this table, compute the following. Be sure to write out the relevant equation for each.
1. The extracted eigenvalue for factor 1.
2. The extracted eigenvalue for factor 2.
3. The extracted communality for item 1.
4. The extracted communality for item 2.
Note that you can verify your computations by comparing your computed values with those presented in the output of the exploratory factor analysis produced.
Table 18.2
Step by Step Answer:
1 The eigenvalue for factor 1 would be computed as follows 664 2 588 2 557 2 451 2 407 2 328 2 22...View the full answer
Measurement Theory In Action
ISBN: 9780367192181
3rd Edition
Authors: Kenneth S Shultz, David Whitney, Michael J Zickar
