Completion (2). Recall from Problem 9.14 that a measure space \((X, \mathscr{A}, \mu)\) is complete if every subset of a \(\mu\)-null set is a \(\mu\)-null set (thus, in particular, measurable). Let \((X, \mathscr{A}, \mu)\)

be a \(\sigma\)-finite measure space - i.e. there is an exhausting sequence \(\left(A_{i}ight)_{i \in \mathbb{N}} \subset \mathscr{A}\) such that \(\mu\left(A_{i}ight)

(i) Show that for every \(Q \subset X\) there is some \(A \in \mathscr{A}\) such that \(\mu^{*}(Q)=\mu(A)\) and that \(\mu(N)=0\) for all \(N \subset A \backslash Q\) with \(N \in \mathscr{A}\).

[ since \(\mu^{*}\) is defined as an infimum, every \(Q\) with \(\mu^{*}(Q)

(ii) Show that \(\left(X, \mathscr{A}^{*},\left.\mu^{*}ight|_{\mathscr{A}} *ight)\) is a complete measure space.

(iii) Show that \(\left.\left(X, \mathscr{A}^{*},\left.\mu^{*}ight|_{\mathscr{A}}ight)^{*}ight)\) is the completion of \((X, \mathscr{A}, \mu)\) in the sense of Problem 4.15 .

Data from problem 9.14

Data from theorem 6.1

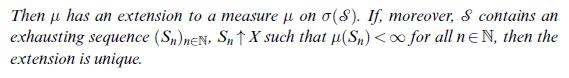
Equation 6.1

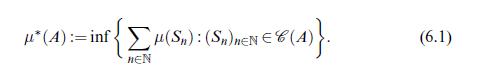
Equation 6.2

(Continuation of Problem 6.3) Consider on R the o-algebra of all Borel sets which are symmetric w.r.t. the origin. Set A+ = An [0, 00), 4:=(-0, 0]n A and consider their symmetrizations 4 = 4 U (-A) . Show that for every u M+ () with 0