Measures Integrals And Martingales 2nd Edition René L. Schilling - Solutions
Discover comprehensive solutions for "Measures Integrals And Martingales 2nd Edition" by René L. Schilling with our extensive online resources. Access the full answers key and solution manual, providing in-depth solutions in PDF format. Explore solved problems and detailed questions and answers tailored for students and instructors. Dive into our test bank and chapter solutions for a thorough understanding. Our step-by-step answers ensure clarity and ease of learning. Whether you need an instructor manual or textbook guidance, our resources are designed to support your academic journey. Enjoy the convenience of free download options to enhance your study experience.
Get 50% OFF
Claim Now
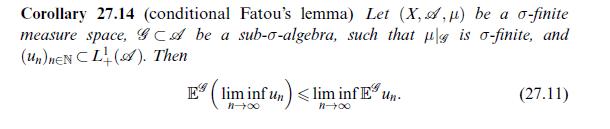
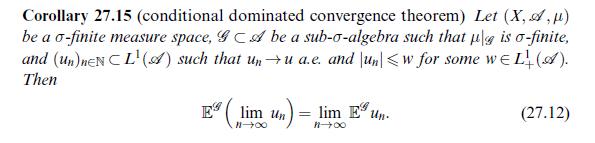
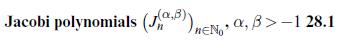
![Theorem 28.6 (Weierstra) Polynomials are dense in C[0, 1] w.r.t. uniform convergence. Proof (S. N. Bernstein)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/8/7/29665af4ce02bec11705987295385.jpg)
![since the function p-p(1-p) attains its maximum at p=1/2. As u C[0, 1] is uniformly continuous, u(x) - u(y) |](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/8/7/30865af4cec958951705987308031.jpg)
![Corollary 28.8 The monomials (t")neN, are complete in L= L ([0, 1], dt), that is, 0,11u(t)t" dt=0 for all](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/8/7/33865af4d0a60c5f1705987337820.jpg)
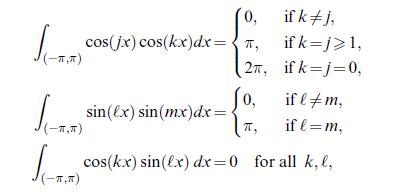
![Theorem 21.5 (Riesz) Let (X,,u) be a o-finite measure space, p = [1,00) and qe (1,00] conjugate indices.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/1/3/97265ae2e74285a01705913971457.jpg)
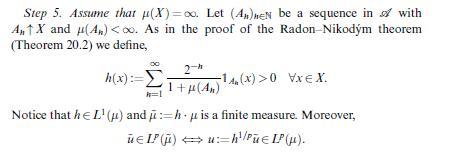
![Theorem 21.5 (Riesz) Let (X, ,) be a o-finite measure space, p = [1,00) and qe (1,00] conjugate indices.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/1/3/86665ae2e0a79cf71705913866010.jpg)
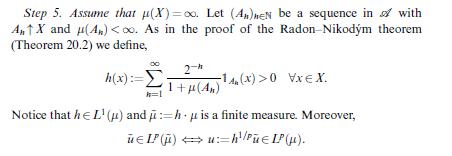
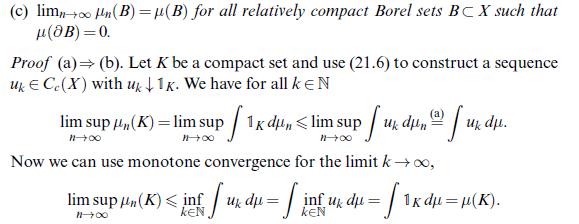
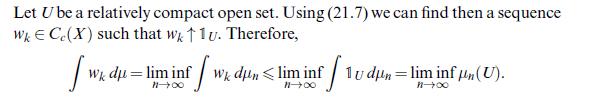
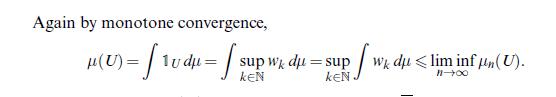
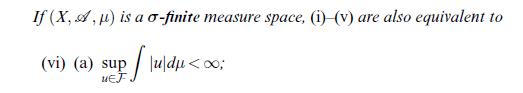
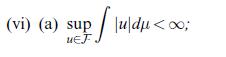
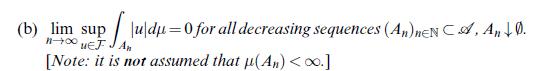
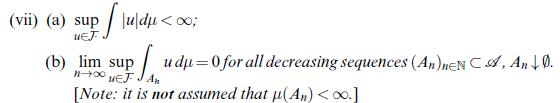
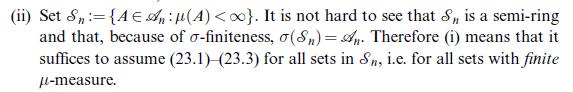
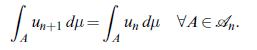
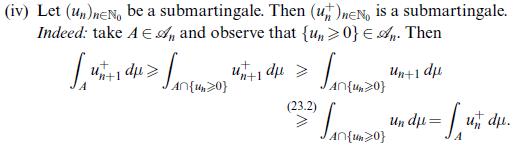
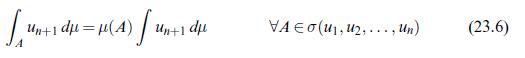
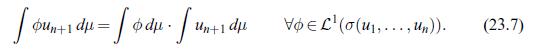
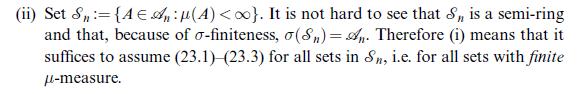
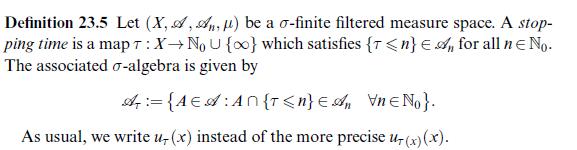
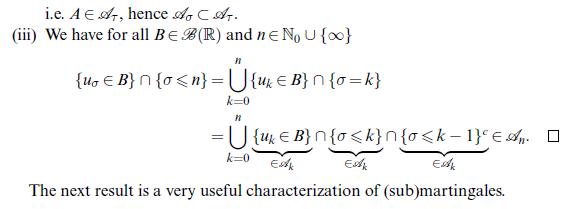
![Lemma 24.1 (Doob's upcrossing estimate) Let (un)neN be a submartingale and denote by U([a, b]; N; x) the](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/2/3/79865ae54d66319d1705923797527.jpg)
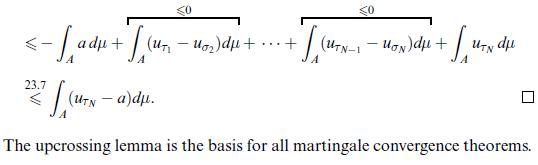
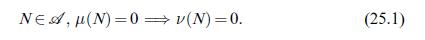
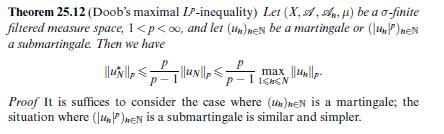
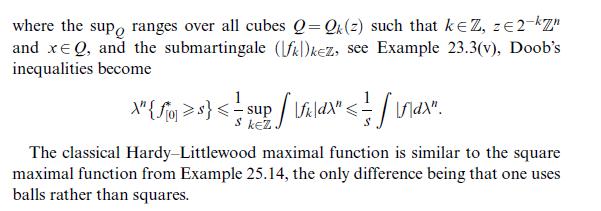
![the restricted maximal function. Since (u-on) 3] 3} } + X"{x:on(x) - u(x) > } Cn "||un||1+0+||on-u||1, where](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/2/5/93965ae5d33345871705925938205.jpg)
