Let (u in mathcal{L}^{2}(mu)) be a positive, integrable function. Show that (int_{{u>1}} u d mu leqslant mu{u>1})
Question:
Let \(u \in \mathcal{L}^{2}(\mu)\) be a positive, integrable function. Show that \(\int_{\{u>1\}} u d \mu \leqslant \mu\{u>1\}\) entails that \(u(x) \leqslant 1\) for \(\mu\)-a.e. \(x\).
Remark. This argument is needed for the second part of the proof of Lemma 27.4 (x).
Data from lemma 27.4 (x)
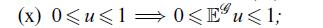
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





