Let ((Omega, mathscr{A}, mathbb{P})) be a probability space and let (left(xi_{n}ight)_{n in mathbb{N}}) be a sequence of
Question:
Let \((\Omega, \mathscr{A}, \mathbb{P})\) be a probability space and let \(\left(\xi_{n}ight)_{n \in \mathbb{N}}\) be a sequence of independent identically distributed random variables with \(\xi_{n} \in \mathcal{L}^{2}(\mathscr{A})\) and \(\int \xi_{n} d \mathbb{P}=0\). Set \(\mathscr{A}_{n}:=\) \(\sigma\left(\xi_{1}, \xi_{2}, \ldots, \xi_{n}ight)\).
(i) Show, without using Example 23.3 (vi), that \(S_{n}^{2}:=\left(\xi_{1}+\xi_{2}+\cdots+\xi_{n}ight)^{2}\) is a submartingale w.r.t. \(\left(\mathscr{A}_{n}ight)_{n \in \mathbb{N}}\).
(ii) Show that there is a constant \(\kappa\) such that \(S_{n}^{2}-\kappa n\) is a martingale w.r.t. \(\left(\mathscr{A}_{n}ight)_{n \in \mathbb{N}}\).
Data from example 23.3 (vi)
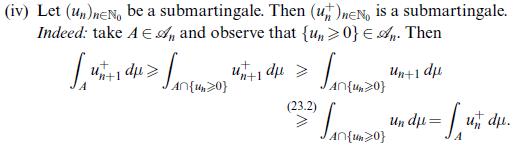
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





