Show that, in the notation of Lemma 23.6 , \(\mathscr{A}_{\sigma \wedge \tau}=\mathscr{A}_{\sigma} \cap \mathscr{A}_{\tau}\) for any two stopping times \(\sigma, \tau\).

Data from lemma 23.6

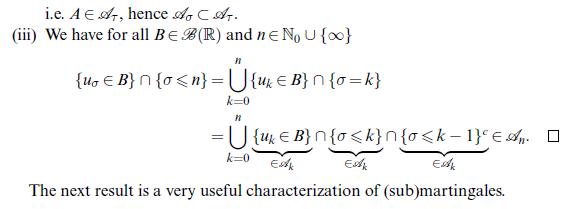
Transcribed Image Text:

Lemma 23.6 Let (X, A, An,) be a o-finite filtered measure space and , T stopping times. (1) O AT, O VT, o+k, ke No are stopping times. (ii) {o