Verify that the random times \(\sigma_{k}\) and \(\tau_{k}\) defined in the proof of Lemma 24.1 are stopping times.

Data from lemma 24.1

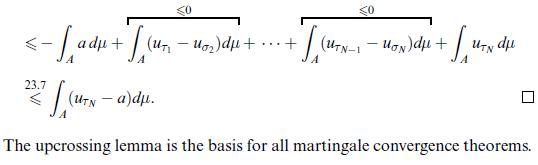
Transcribed Image Text:

Lemma 24.1 (Doob's upcrossing estimate) Let (un)neN be a submartingale and denote by U([a, b]; N; x) the number of upcrossings of (un(x))neNo across [a, b] which occur for the indices 0 b} ^N; as usual we set inf=+o. Writing U=U([a, b]; N), we find that To=0 <01 <7 <0