Show the following improvement of Doob's maximal inequality Theorem 25.12 . Let (left(u_{n}ight)_{n in mathbb{N}}) be a
Question:
Show the following improvement of Doob's maximal inequality Theorem 25.12 . Let \(\left(u_{n}ight)_{n \in \mathbb{N}}\) be a martingale or \(\left(\left|u_{n}ight|^{p}ight)_{n \in \mathbb{N}}, 1
\[\max _{n \leqslant N}\left\|u_{n}ight\|_{p} \leqslant\left\|u_{N}^{*}ight\|_{p} \leqslant \frac{p}{p-1}\left\|u_{N}ight\|_{p} \leqslant \frac{p}{p-1} \max _{1 \leqslant n \leqslant N}\left\|u_{n}ight\|_{p} .\]
Data from theorem 25.12
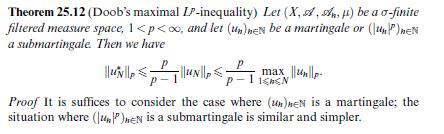

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





