Weak convergence in (L^{p}). Let ((X, mathscr{A}, mu)) be a (sigma)-finite measure space and let (p in(1,
Question:
Weak convergence in \(L^{p}\). Let \((X, \mathscr{A}, \mu)\) be a \(\sigma\)-finite measure space and let \(p \in(1, \infty]\), \(q \in[1, \infty)\) be conjugate indices. We assume that \(L^{q}(\mu)\) is separable, containing the countable dense set \(\mathcal{D}_{q}\).
(i) If \(\left(u_{n}ight)_{n \in \mathbb{N}}\) is bounded in \(L^{p}\), i.e. \(\sup _{n}\left\|u_{n}ight\|_{p}
[ use the Bolzano-Weierstraß theorem and a diagonal argument.]
(ii) The limit in part (i) exists for all \(g \in L^{q}(\mu)\).
(iii) Conclude from parts (i) and (ii) that there exists a function \(u \in L^{p}(\mu)\) such that \(\lim _{i} \int u_{n(i)} g d \mu=\int u g d \mu\) ('weak convergence in \(L^{p}\) '). This proves the following result: every \(L^{p}\)-bounded sequence has a weakly convergent subsequence.
[set \(g \mapsto I(g):=\lim _{i} \int u_{n(i)} g d \mu\) and use Theorem 21.5 , hence the restriction \(p>1\).]
Data from theorem 21.5
![Theorem 21.5 (Riesz) Let (X, ,) be a o-finite measure space, p = [1,00) and qe (1,00] conjugate indices.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/1/3/86665ae2e0a79cf71705913866010.jpg)

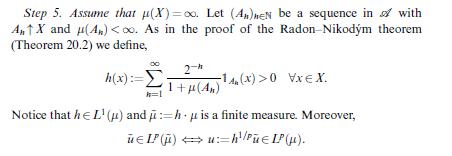

Step by Step Answer:






