Let (left(u_{n}, mathscr{A}_{n}ight)_{n in mathbb{N}}) be a martingale with (u_{n} in mathcal{L}^{2}left(mathscr{A}_{n}ight)). Show that [int u_{n} u_{k}
Question:
Let \(\left(u_{n}, \mathscr{A}_{n}ight)_{n \in \mathbb{N}}\) be a martingale with \(u_{n} \in \mathcal{L}^{2}\left(\mathscr{A}_{n}ight)\). Show that
\[\int u_{n} u_{k} d \mu=\int u_{n \wedge k}^{2} d \mu\]
[ assume that \(n Equation 23.1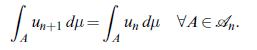
Transcribed Image Text:
-=_ p "n" [=1p1+"n"
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 100% (2 reviews)
Data from lemma 172 Using Lemma 172 we can approximate u E L by simple functions i...View the full answer

Answered By

Utsab mitra
I have the expertise to deliver these subjects to college and higher-level students. The services would involve only solving assignments, homework help, and others.
I have experience in delivering these subjects for the last 6 years on a freelancing basis in different companies around the globe. I am CMA certified and CGMA UK. I have professional experience of 18 years in the industry involved in the manufacturing company and IT implementation experience of over 12 years.
I have delivered this help to students effortlessly, which is essential to give the students a good grade in their studies.
3.50+
2+ Reviews
10+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Business questions
-
An object of mass m is released from rest at height 3R above the ground and slides down the frictionless vertical track as shown. The corner is a frictionless quarter-circle track of radius R. At the...
-
You play a sequence of independent games each of which you win probability p and lose with probability q = 1-p. You start with 2k and stop when you reach 2m or 0, where 0
-
First, identify a service industry of mine is, General Motors. Then, in a short paper, do the following: Why does General Motors start production on the Camaro and, after a few years, decide to stop...
-
If there is a decrease in the demand for Canadian dollars relative to U.S. dollars, a. The price and quantity of Canadian dollars traded will fall. b. The price and quantity of Canadian dollars will...
-
Show that the number of different electron states possible for a given value of n is 2n2.
-
What are [Ba2+] and [SO42] in a saturated solution of BaSO4? The Ksp of BaSO4 is 1.1 1010.
-
Service workers and customer relations. A study in Industrial Marketing Management (February 2016) investigated the impact of service workers (e.g., waiters and waitresses) personal resources on the...
-
Even though firms follow the accounting rules (GAAP) when presenting their financial statements it is still possible for conflicts of interest to exist between what management wants investors and...
-
Here are selected 2022 transactions of Sunland Corporation Jan 1 June 30 Retired a piece of equipment that was purchased on January 1, 2012. The equipment cost $82,500 and had a useful life of 10...
-
Martingale transform. Let \(\left(u_{n}, \mathscr{A}_{n}ight)_{n \in \mathbb{N}}\) be a martingale and let \(\left(f_{n}ight)_{n \in \mathbb{N}}\) be a sequence of bounded functions such that \(f_{n}...
-
Prove the assertion made in Remark 23.2 (ii). Data from remark 23.2 (ii) (ii) Set Sn = {AE An: (A)
-
What trends in the enterprise market are affecting BBRY (BlackBerry)?
-
Show how you would go about balancing the following equations: Cu + HNO3 Cu(NO3)2 + NO + H2O HIO3 + Fel2 + HCI FeCl3 + ICI + H2O 2.Conservation of mass A student places 0.58 g of iron and 1.600 g...
-
Sales MOSS COMPANY Income Statement For Year Ended December 31, 2021 Cost of goods sold Gross profit Operating expenses (excluding depreciation) Depreciation expense Income before taxes Income taxes...
-
Prior to the Covid-19 epidemic, Master's and Ph.D. programs in psychology required applying students to submit their scores on the standardized graduate admission exam (GRE). For the past three...
-
Benicio wants to make sure that the Sales table does not contain any duplicate records, which would make any sales analysis incorrect. Identify and remove duplicate records in the Sales table as...
-
University Car Wash purchased new soap dispensing equipment that cost $261,000 including installation. The company estimates that the equipment will have a residual value of $27,000. University Car...
-
Methane gas (CH4) at 25C is burned with the stoichiometric amount of air at 25C during an adiabatic steady-flow combustion process at 1 atm. Assuming the product gases consist of CO2, H2O, CO, N2,...
-
Explain the Hawthorne effect.
-
The balance in Amber Companys work-in-process inventory account was $400,000 at the beginning of September and $320,000 at the end of September. Manufacturing costs for the month follow. Required:...
-
Boulder Products, Inc., had the following activity for the month of October. Required: Prepare an income statement for the month of October. Sales revenue Selling expenses General and administrative...
-
Home Depots annual report appears as follows in summary form. (This information was obtained from the companys Web site, www.homedepot.com. Required: a. The financial information in the companys...
-
Sweeten Company had no jobs in progress at the beginning of March and no beginning inventories. The company has two manufacturing departments --Molding and Fabrication. It started, completed, and...
-
Horizontal Analysis The comparative accounts payable and long-term debt balances of a company are provided below. Current Year Previous Year Accounts payable $47,286 $63,900 Long-term debt 85,492...
-
On January 1, Year 1, Price Company issued $140,000 of five-year, 7 percent bonds at 97. Interest is payable annually on December 31. The discount is amortized using the straight-line method. Record...

Study smarter with the SolutionInn App


