(Continuation of Problem 26.2 ) Assume now that (W) is a (mathbb{C})-vector space with norm (|cdot|) satisfying...
Question:
(Continuation of Problem 26.2 ) Assume now that \(W\) is a \(\mathbb{C}\)-vector space with norm \(\|\cdot\|\) satisfying the parallelogram identity (26.3) and let
\[(v, w)_{\mathbb{R}}:=\frac{1}{4}\left(\|v+w\|^{2}-\|v-w\|^{2}ight)\]
Then \((v, w)_{\mathbb{C}}:=(v, w)_{\mathbb{R}}+i(v, i w)_{\mathbb{R}}\) is a complex-valued inner product.
Data from problem 26.2
This exercise shows the following theorem. Theorem (Fréchet-von Neumann-Jordan). An inner product \(\langle\cdot, \cdotangle\) on the \(\mathbb{R}\)-vector space \(V\) derives from a norm if, and only if, the parallelogram identity (26.3) holds.
Equation 26.3
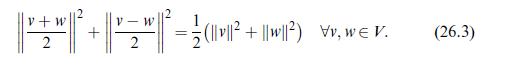
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





