Let (X=mathbb{R}^{n}) (or a separable metric space). Let (B) be a Borel set or, more generally, an
Question:
Let \(X=\mathbb{R}^{n}\) (or a separable metric space). Let \(B\) be a Borel set or, more generally, an \(\overline{\mathcal{H}}^{\phi}\)-measurable set, such that \(\mathcal{H}(B)
[Instructions. Open sets in \(X\) are \(F_{\sigma}\)-sets. Thus, Corollary 18.10 gives a decreasing sequence \(U_{i} \supset B\) of open sets and increasing sequences \(F_{i k} \uparrow U_{i}\) of closed sets. Show that \(\mathcal{H}^{\phi}\left(B \backslash F_{i k(i)}ight) \leqslant \epsilon / 2^{i}\), define \(F=\bigcap_{i} F_{i k(i)}\) and verify \(\mathcal{H}^{\phi}(F \backslash B)=0\). According to Corollary \(18.10 F \backslash B\) is contained in a \(G_{\delta}\)-set \(G\) with \(\mathcal{H}^{\phi}(G)=0\), the \(F_{\sigma}\)-set \(F \backslash G\) is in \(B\) and has the same Hausdorff measure.]
Data from corollary 18.10
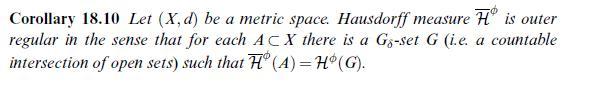

Step by Step Answer:






