Modify the proof of Theorem 15.11 and show that \(C_{c}^{\infty}\left(\mathbb{R}^{n}ight)\) is uniformly dense in \(C_{c}\left(\mathbb{R}^{n}ight)\).

Data from theorem 15.11

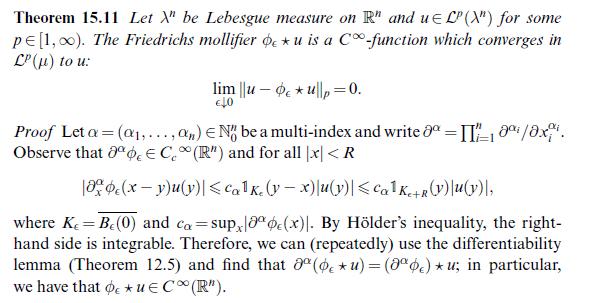
Transcribed Image Text:

Theorem 15.11 Let X" be Lebesgue measure on R" and uELP (X") for some pe [1,00). The Friedrichs mollifier ou is a C-function which converges in LP () to u: eup=0. Proof Let a = (a,...,an) No be a multi-index and write = 10/8x. Observe that a EC (R") and for all |x|