Prove the following result of W.H. Young [60]; among statisticians it is also known as Pratt's lemma,
Question:
Prove the following result of W.H. Young [60]; among statisticians it is also known as Pratt's lemma, see J. W. Pratt [38].
Theorem (Young; Pratt). Let and be sequences of integrable functions on a measure space . If
(a) for all ,
(b) for all and all ,
(c) and with and finite,
then and is finite.
Explain why this generalizes Lebesgue's dominated convergence theorem, Theorem 12.2 (ii).
Data from theorem 12.2
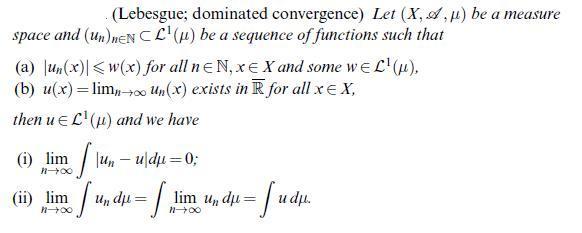

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





