An approximate solution of a multi-degree-of-freedom system can be obtained using the mode acceleration method. According to this method, the equations of motion of an undamped system, for example, are expressed as

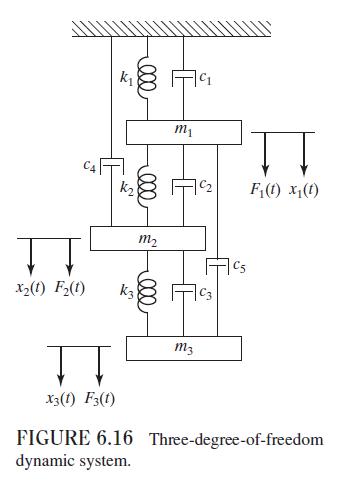
and \(\ddot{\vec{x}}\) is approximated using the first \(r\) modes \((r

Since \(\left([k]-\omega_{i}^{2}[m]\right) \vec{X}^{(i)}=\overrightarrow{0}\), Eq. (E.1) can be written as

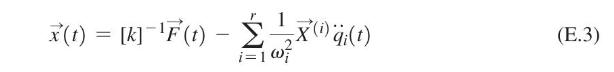
Find the approximate response of the system described in Example 6.19 (without damping), using the mode acceleration method with \(r=1\).

Data From Example 6.19:-

Figure 6.16:-

x = [k](F-[m]x) (E.1)