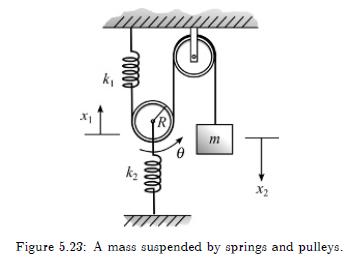
Consider again the system shown in Figure 2.58, reproduced in Figure 5.23. The system consists of massless
Question:
Consider again the system shown in Figure 2.58, reproduced in Figure 5.23. The system consists of massless pulleys, a block of mass \(m\), and two linear springs. The coordinate, \(\theta\), is the angle of rotation of the moving pulley, \(x_{1}\) is the displacement of the pulley center of mass, and \(x_{2}\) is the displacement of the mass. The displacements are measured from the positions where the springs are undeformed.
(a) Find the static equilibrium position of the system using the principle of virtual work, and
(b) derive the equation of motion of the system using d'Alembert's principle for generalized coordinate \(x_{2}\).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Mechanical Vibration Analysis, Uncertainties, And Control
ISBN: 9781498753012
4th Edition
Authors: Haym Benaroya, Mark L Nagurka, Seon Mi Han
Question Posted:





