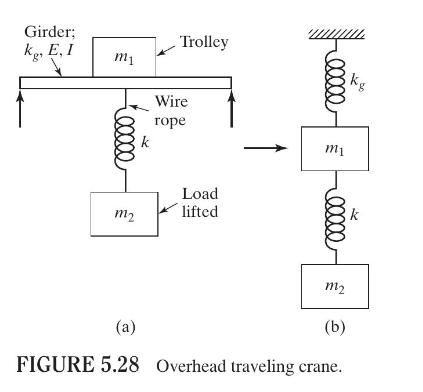
Consider the overhead traveling crane described in Problem 5.9 (Fig. 5.28). If the rails on both sides of the girder have a sinusoidally varying surface in the \(z\) direction (perpendicular to the page), as shown in Fig. 5.44, set up the equations and the initial conditions for finding the vibration response of the load lifted \((m)\) in the vertical direction. Assume that the velocity of the crane is \(10 \mathrm{~m} / \mathrm{min}\) in the \(z\) direction.

Data From Problem 5.9:-

An electric overhead traveling crane, consisting of a girder, trolley, and wire rope, is shown in Fig. 5.28. The girder has a flexural rigidity \((E I)\) of \(17 \times 10^{9} \mathrm{~N}-\mathrm{m}^{2}\) and a span \((L)\) of \(10 \mathrm{~m}\). The rope is made of steel and has a length \((l)\) of \(7 \mathrm{~m}\). The masses of the trolley and the load lifted are \(4000 \mathrm{~kg}\) and \(1000 \mathrm{~kg}\), respectively. Find the area of cross section of the rope such that the fundamental natural frequency is greater than \(20 \mathrm{~Hz}\).

Transcribed Image Text:

$5 cm 3 m FIGURE 5.44 Motion of traveling crane.