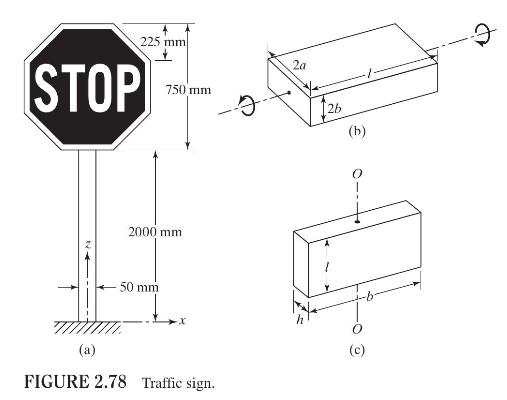
Figure 2.78 (a) shows a steel traffic sign, of thickness (3 mathrm{~mm}) fixed to a steel post.
Question:
Figure 2.78 (a) shows a steel traffic sign, of thickness \(3 \mathrm{~mm}\) fixed to a steel post. The post is \(2 \mathrm{~m}\) high with a cross section \(50 \mathrm{~mm} \times 6 \mathrm{~mm}\), and it can undergo torsional vibration (about the \(z\)-axis) or bending vibration (either in the \(z x\)-plane or the \(y z\)-plane). Determine the mode of vibration of the post in a storm during which the wind velocity has a frequency component of \(1.25 \mathrm{~Hz}\).
1. Neglect the weight of the post in finding the natural frequencies of vibration.
2. Torsional stiffness of a shaft with a rectangular section (see Fig. 2.78(b)) is given by
\[k_{t}=5.33 \frac{a b^{3} G}{l}\left[1-0.63 \frac{b}{a}\left(1-\frac{b^{4}}{12 a^{4}}\right)\right]\]
where \(G\) is the shear modulus.
3. Mass moment of inertia of a rectangular block about axis \(O O\) (see Fig. 2.78(c)) is given by
\[I_{O O}=\frac{ho l}{3}\left(b^{3} h+h^{3} b\right)\]
where \(ho\) is the density of the block.
Step by Step Answer:






