Find the free-vibration response of the three-degree-of-freedom airplane model considered in Problem 6.10 for the following data: \(m=5000 \mathrm{~kg}, l=5 \mathrm{~m}, E=7 \mathrm{GPa}, I=8 \times 10^{-6} \mathrm{~m}^{4}\). Assume that the initial conditions correspond to that of a gust which results in \(x_{1}(0)=0\), \(x_{2}(0)=0.1 \mathrm{~m}, x_{3}(0)=0, \dot{x}_{1}(0)=\dot{x}_{2}(0)=\dot{x}_{3}=0\).

Data From Problem 6.10:-

For a simplified analysis of the vibration of an airplane in the vertical direction, a threedegree-of-freedom model, as shown in Fig. 6.26, can be used. The three masses indicate the masses of the two wings \(\left(m_{1}=m_{3}=m\right)\) and the fuselage \(\left(m_{2}=5 m\right)\). The stiffnesses

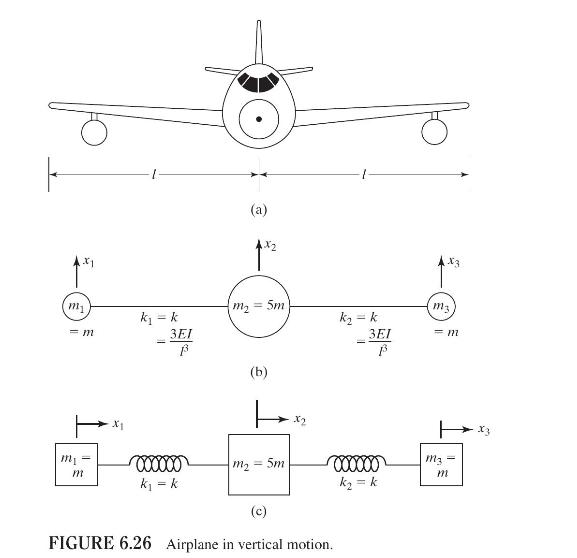
\(k_{1}=k_{2}=k\) correspond to the bending stiffnesses of the two wings, which can be modeled as cantilever beams so that \(k_{1}=k_{2}=k=\frac{3 E I}{l^{3}}\).

a. Derive the equations of motion of the airplane using the three-degree-of-freedom model.

b. Using the equations of motion derived in part (a), find the natural frequencies and mode shapes of the airplane. Give an interpretation of the results.

Transcribed Image Text:

(a) x3 my m = 5m m3 = k k = k = m 3E1 3EI = m mi m = (b) 000000 k = k m2 = 5m 000000 k = M3 m = k (c) FIGURE 6.26 Airplane in vertical motion.