For Problem 26, estimate the first two natural frequencies using the Rayleigh-Ritz procedure. Assume a trial function of the form \(\mathcal{Y}(x)=c_{1} x^{2}+c_{2} x^{3}\). Compare the fundamental frequencies estimated by the Rayleigh-Ritz and the Rayleigh quotient methods.

Problem 26:

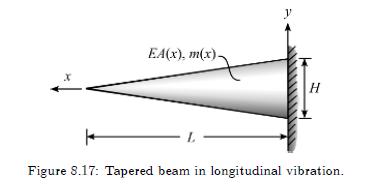
Estimate the fundamental frequency for the tapered beam of Figure 8.17 where

\[ m(x)=m(1-x / L) \]

and

\[ E A(x)=E A(1-x / L) \]

Compare your result to the exact value of \(\omega_{1}=\) \(2.40 \sqrt{E A / m L^{2}}\).

X EA(x), m(x)- y H L Figure 8.17: Tapered beam in longitudinal vibration.