If Problem 36 is modified to include damping between the two masses as shown in Figure 6.77, solve for the case with no forcing using

(a) modal analysis, and

(b) the direct method.

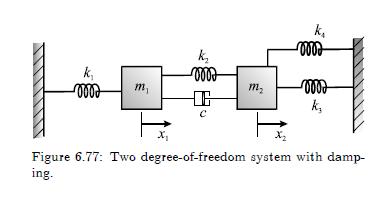
Problem 36:

For the two degree-of-freedom system in Figure 6.76 undergoing longitudinal motion, derive the equations of motion utilizing each of the following approaches:

(a) flexibility coefficients,

(b) Newton's second law of motion,

(c) Lagrange's equation, and

(d) Hamilton's principle. Then, with the equations of motion in matrix form, derive the natural frequencies and mode shapes, and solve for the responses.

Assume the values \(m_{1}=m_{2}=1 \mathrm{~kg}\) and all stiffnesses are \(1 \mathrm{~N} / \mathrm{m}\). Solve via (i) the direct method and (ii) modal analysis.

Find the response of each mass if the initial velocities equal zero and the initial displacements are in the ratio of the first mode. For a design application, it is necessary that \(\left|x_{2}-x_{1}\right| \geq x_{c r}\), where \(x_{c r}\) is some critical separation distance between the masses. Describe how to check that this condition is met, and what options exist for redesign of the system or feedback control if the condition is not met.

0000 k mo 0002 m m oood C k x Figure 6.77: Two degree-of-freedom system with damp- ing.