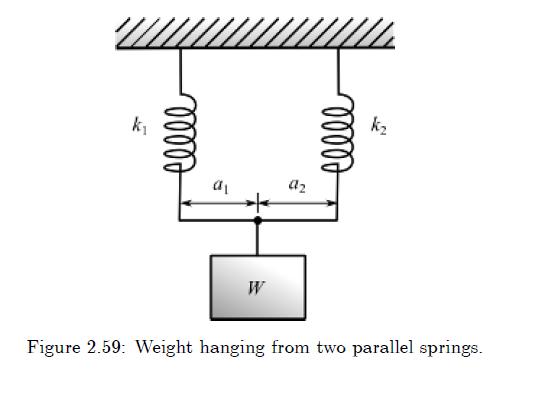
Show that the period of free vibration of a load weighing \(W\) suspended from two parallel springs, as shown in Figure 2.59, is given by \(T\),

\[ T=2 \pi \sqrt{\frac{W}{g\left(k_{1}+k_{2}\right)}} \]

and show that the equivalent stiffness is \(k=k_{1}+k_{2}\). Discuss the need to hang the weight asymmetrically, that is \(a_{1} eq a_{2}\) if \(k_{1} eq k_{2}\), so that the extension of the springs is identical and that the ratio \(a_{1} / a_{2}=\) \(k_{2} / k_{1}\).

Transcribed Image Text:

k F a W a eeeee F Figure 2.59: Weight hanging from two parallel springs.