Structures are sometimes subjected to very rapidly applied loads of extremely short duration. These types of loads are called blast or explosive loads. Consider how such a load time history may look. Figure 4.33

(a) is a generic blast load. There is a rapid rise time along with an exponential-like decay, and by time \(t_{1}\) the load is effectively zero, where \(t_{1} \ll 1 \mathrm{~s}\). Such a time history is generally a very complicated function that may not be easily determined because of its sensitivity to many factors, such as the medium through which the load passes, be it the atmosphere or the Earth.

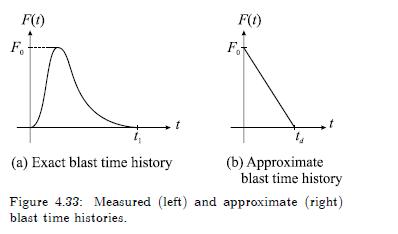
A common approach is to curve-fit the time history with an appropriate combination of functions. As a first approximation here, we replace the exact curve by the one shown in Figure 4.33(b). To draw such a straight-line approximation, estimate the area under the original curve (this is the impulse) and set it equal to the area under the triangle load, thus fixing the value of \(t_{d}\). The maximum value \(F_{0}\) is the same for both curves. Although not strictly true for such high strain-rate loading, we neglect the effects of damping for the early time response. Solve for the structural response for all time; \(0 \leq t \leq t_{d}\) and \(t \geq t_{d}\). Show that:
\[ \begin{aligned} x(t)= & \frac{F_{0}}{m \omega_{n}^{2}}\left\{1-\frac{t}{t_{d}}-\cos \omega_{n} t\right. \\ & \left.+\left(\frac{1}{\omega_{n} t_{d}}\right) \sin \omega_{n} t\right\}, 0 \leq t \leq t_{d} \\ x(t)= & \frac{F_{0}}{m \omega_{n}^{3} t_{d}}\left\{\sin \omega_{n} t\left(1-\cos \omega_{n} t_{d}\right)\right. \\ & \left.-\cos \omega_{n} t\left(\omega_{n} t_{d}-\sin \omega_{n} t_{d}\right)\right\}, t>t_{d} \end{aligned} \]

Transcribed Image Text:

Fo F(t) t F(t) Fo (a) Exact blast time history (b) Approximate blast time history Figure 4.33: Measured (left) and approximate (right) blast time histories.