The force transmissibility of a damped single-degree-of-freedom system with base motion is given by Eq. (9.106): [T_{f}=frac{F_{t}}{k
Question:
The force transmissibility of a damped single-degree-of-freedom system with base motion is given by Eq. (9.106):
\[T_{f}=\frac{F_{t}}{k Y}=r^{2}\left\{\frac{1+(2 \zeta r)^{2}}{\left(1-r^{2}\right)^{2}+(2 \zeta r)^{2}}\right\}^{\frac{1}{2}}\]
where \(F_{t}\) is the magnitude of the force transmitted to the mass. Determine the frequency ratios (r) at which the force transmissibility attains maximum and minimum values. Discuss your results.
Equation 9.106:-
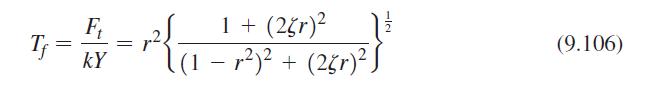
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





