The mean square value of the response of a machine, (Eleft[y^{2} ight]), subject to the force shown
Question:
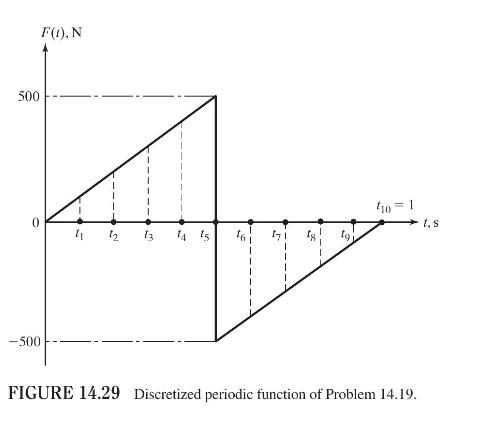
The mean square value of the response of a machine, \(E\left[y^{2}\right]\), subject to the force shown in Fig. 14.29, is given by (see Problem 14.26):
\[E\left[y^{2}\right]=\sum_{n=0}^{N-1} \frac{\left|c_{n}\right|^{2}}{\left(k-m \omega_{n}^{2}\right)^{2}+c^{2} \omega_{n}^{2}}\]
where
\[c_{n}=\frac{1}{N} \sum_{j=1}^{N} F_{j}\left\{\cos \frac{2 \pi n j}{N}-i \sin \frac{2 \pi n j}{N}\right\}\]
with \(F_{j}=0,100,200,300,400,500,-400,-300,-200,-100,0\) for \(j=0,1,2,3,4,5,6\), \(7,8,9,10 ; k=4 \times 10^{4}, c=1200, m=5.1760\), and \(\omega_{n}=2 \pi n\). Using MATLAB, find the value of \(E\left[y^{2}\right]\) with \(N=10\).
Data From Problem 14.26:-
A machine, modeled as a single-degree-of-freedom system, has the following parameters: \(m=900 \mathrm{~kg}, k=7 \mathrm{MN} / \mathrm{m}\), and \(c=135 \mathrm{~N}-\mathrm{s} / \mathrm{m}\). It is subjected to the force shown in Fig. 14.29. Find the mean square value of the response of the machine (mass).
Figure 14.29:-
Step by Step Answer:






