The response of a system excited at its base by \(y(t)=Y \sin \omega t\) is given by

\[ x(t)=X \sin \left(\omega_{b} t-\phi\right) \]

with

\[ \frac{X}{Y}=\left[\frac{1+\left(2 \zeta \omega_{b} / \omega_{n}\right)^{2}}{\left(1-\omega_{b}^{2} / \omega_{n}^{2}\right)^{2}+\left(2 \zeta \omega_{b} / \omega_{n}\right)^{2}}\right]^{1 / 2} \]

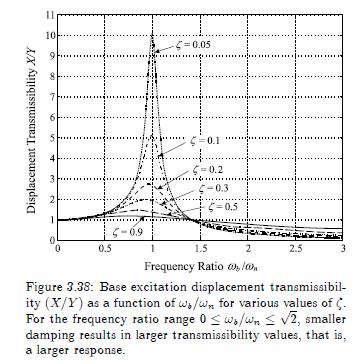
Use Figure 3.38 for displacement transmissibility in answering the following questions. (Do not solve any equations.) Assume negligible damping.

(a) Assume that the maximum amplitude of the base is \(Y=1 \mathrm{~cm}\). A design for a rotating machine with this value of \(Y\) and with natural frequency \(\omega_{n}=\) \(3 \mathrm{rad} / \mathrm{s}\) is required so that \(X \leq 2 \mathrm{~cm}\) across all frequencies \(\omega_{b}\). Which \(\zeta\) value should be chosen?

(b) Suppose that instead of the criteria in (a), we require \(X \leq 1 \mathrm{~cm}\) and \(\zeta

(c) What is the equation for the maximum force transmitted to the base in terms of \(\zeta,\left(\omega_{b} / \omega_{n}\right), k\), and \(Y\) ? For \(\zeta=1.0\), what is the force transmissibility \(\left(F_{T} / k Y\right)\) when the machine is running at \(\omega_{b} \simeq 0\), \(\omega_{b}=3 \sqrt{2} \mathrm{rad} / \mathrm{s}\), and \(\omega_{b}=9 \mathrm{rad} / \mathrm{s}\) ?

Transcribed Image Text:

11 10 a 00 6 Displacement Transmissibility X/Y 5 + 3 2 1 -0.05 0.9 0.5 1 5=0.1 5 0.2 5-0.3 =0.5 1.5 2 2.5 3 Frequency Ratio 0,/ Figure 3.38: Base excitation displacement transmissibil- ity (X/Y) as a function of w/w for various values of (. For the frequency ratio range 0wo/wn 2, smaller damping results in larger transmissibility values, that is, a larger response.