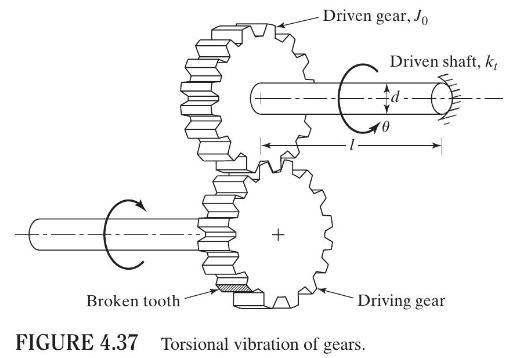
The torsional vibrations of a driven gear mounted on a shaft (see Fig. 4.37) under steady conditions
Question:
The torsional vibrations of a driven gear mounted on a shaft (see Fig. 4.37) under steady conditions are governed by the equation
\[J_{0} \ddot{\theta}+k_{t} \theta=M_{t}\]
where \(k_{t}\) is the torsional stiffness of the driven shaft, \(M_{t}\) is the torque transmitted, \(J_{0}\) is the mass moment of inertia, and \(\theta\) is the angular deflection of the driven gear. If one of the 16 teeth on the driving gear breaks, determine the resulting torsional vibration of the driven gear for the following data.
Driven gear: \(J_{0}=0.1 \mathrm{~N}-\mathrm{m}-\mathrm{s}^{2}\), speed \(=1000 \mathrm{rpm}\), driven shaft: material-steel, solid circular section with diameter \(5 \mathrm{~cm}\) and length \(1 \mathrm{~m}, M_{t 0}=1000 \mathrm{~N}-\mathrm{m}\).
Step by Step Answer:






