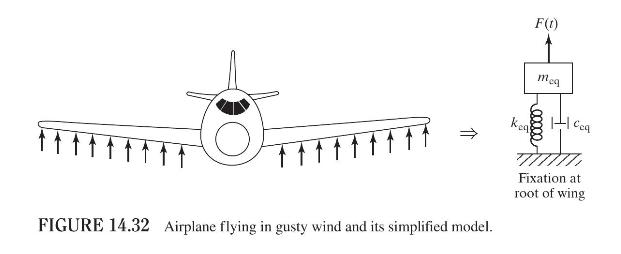
The wing of an airplane flying in gusty wind has been modeled as a spring-mass-damper system, as shown in Fig. 14.32. The undamped and damped natural frequencies of the wing are found to be \(\omega_{1}\) and \(\omega_{2}\), respectively. The mean square value of the displacement of \(m_{\mathrm{eq}}\) (i.e., the wing) is observed to be \(\delta\) under the action of the random wind force whose power spectral density is given by \(S(\omega)=S_{0}\). Derive expressions for the system parameters \(m_{\mathrm{eq}}, k_{\mathrm{eq}}\), and \(c_{\mathrm{eq}}\) in terms of \(\omega_{1}, \omega_{2}, \delta\), and \(S_{0}\).

Transcribed Image Text:

F(t) mcg Ceq FIGURE 14.32 Airplane flying in gusty wind and its simplified model. Fixation at root of wing