Using the fundamental relation between input and output spectra, find the response spectrum for the oscillator governed by

\[\ddot{X}+2 \zeta \omega_{n} \dot{X}+\omega_{n}^{2} X=\frac{1}{m} F(t)\]

with \(m=10 \mathrm{~N}, \zeta=0.15, k=5 \mathrm{~N} / \mathrm{m}\), where the spectrum for \(F(t)\) is (a) the Pierson-Moskowitz (Equation 9.33), with wind speed \(V=25 \mathrm{~km} / \mathrm{h}\), and (b) the wind spectrum (Equation 9.34) where \(\bar{V}_{10}=20 \mathrm{mi} / \mathrm{h}\), and \(\kappa=0.01\). For each, numerically evaluate the mean-square response and plot each response spectrum.

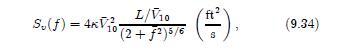
Snn (w) = 8.1 x 10-g ws exp-0.74 -0.7 (1)* ms, ms, (9.33)