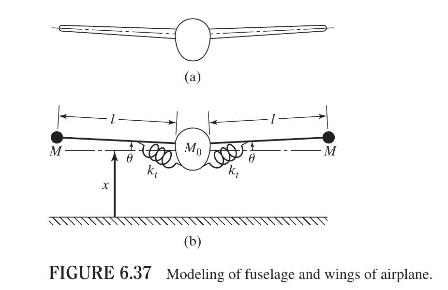
When an airplane (see Fig. 6.37(a)) undergoes symmetric vibrations, the fuselage can be idealized as a concentrated central mass \(M_{0}\) and the wings can be modeled as rigid bars carrying end masses \(M\), as shown in Fig. 6.37(b). The flexibility between the wings and the fuselage can be represented by two torsional springs of stiffness \(k_{t}\) each.

(a) Derive the equations of motion of the airplane, using Lagrange's equations with \(x\) and \(\theta\) as generalized coordinates.

(b) Find the natural frequencies and mode shapes of the airplane.

(c) Find the torsional spring constant in order to have the natural frequency of vibration, in torsional mode, greater than \(2 \mathrm{~Hz}\) when \(M_{0}=1000 \mathrm{~kg}, M=500 \mathrm{~kg}\), and \(l=6 \mathrm{~m}\).

Transcribed Image Text:

M x (a) M Mo Ki wwwwww (b) FIGURE 6.37 Modeling of fuselage and wings of airplane.