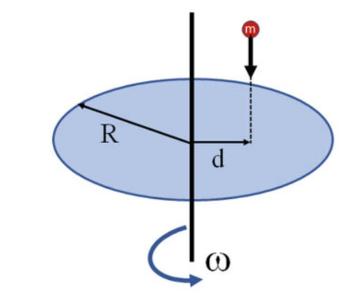
A homogeneous disk of mass \(M=300 \mathrm{~g}\) and radius \(R=23.0 \mathrm{~cm}\) rotates with constant angular speed \(\omega_{0}=25.0 \mathrm{rad} / \mathrm{s}\) around a fixed vertical axis, coincident with its geometric axis, Fig. 12.14. The disk is fixed to the axis and is constrained to rotate in a horizontal plane. By symmetry, under these conditions, the axis is not stressed by any radial force. At a certain instant, a projectile of mass \(m=28.0 \mathrm{~g}\) is fired at the disk, sticking to it (completely inelastic impact). The projectile (considered point-like) has velocity \(v=40 \mathrm{~km} / \mathrm{h}\) parallel to the axis of rotation of the disk and distance \(d=19.0 \mathrm{~cm}\) from it (see figure).
1. Calculate the value of the magnitude of the angular momentum of the rotating disk before the collision;
2. determine the angular speed of the disk after the impact;
3. determine the amount of energy lost in the impact process;
4. determine the radial force with which the axis of rotation is stressed in the final situation, with the projectile embedded in the disc. Justify why this radial force must exist.

Fig. 12.14

Transcribed Image Text:

R d @ m