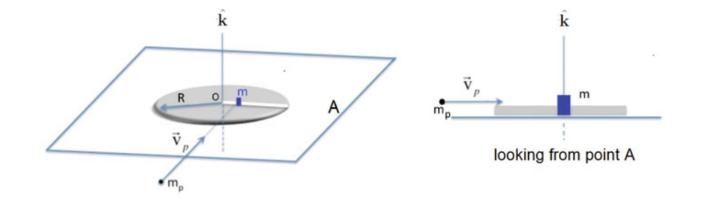
The system in Fig.12.21 consists of a homogeneous disk of mass \(M=300 \mathrm{~g}\) and radius \(R=40.0 \mathrm{~cm}\). At the disk, a slit has been produced along the entire length \(R\) of the disk, obtained by removing a bar of mass equal to \(1 / 20\) of \(M\) from the disk. Into the radial slit is inserted a cube of mass \(m=40.0 \mathrm{~g}\). The cube is initially at distance \(R / 3\) from center \(\mathrm{O}\) and is constrained to slide without friction along the slit. The disk, in the horizontal plane, can rotate without friction about a fixed vertical axis passing through \(\mathrm{O}\). With respect to this axis, calculate:

1. the moment of inertia of the system, neglecting effects due to the transverse dimensions of the slit and considering the cube to be point-like.

2. The initially stationary system is then struck by a projectile of mass \(m_{P}=20.0 \mathrm{~g}\), which sticks into the cube; the cube protrudes from the surface of the disk as shown in the figure. Before the impact, the projectile has speed \(v_{P}=40.0 \mathrm{~m} / \mathrm{s}\) in the plane of the disk, directed orthogonally to the slit as in the figure. Determine the angular speed \(\omega_{1}\) of the disk immediately after the impact.

3. Next, the block with the projectile in it slides (without friction) along the slit until it is ejected. Calculate, for the instant the cube reaches the edge, the angular speed \(\omega_{2}\) of the disc and 4. the radial speed of the cube.

Fig. 12.21

Transcribed Image Text:

mp k k A mp. looking from point A