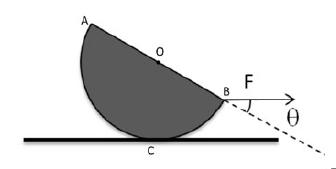
A homogeneous hemisphere, mass \(m=170 \mathrm{~g}\) and radius \(R=3.0 \mathrm{~cm}\), is placed on a horizontal plane and it is pulled by a horizontal force \(\mathbf{F}\), of unknown magnitude, applied at the point B (see Fig. 7.16). In these conditions the hemisphere moves with constant speed without oscillations, inclined by an unknown angle \(\theta\) with respect to the equilibrium position. The coefficient of dynamic friction between the hemisphere and the horizontal plane is \(\mu_{d}=0.25\). The center of mass of the hemisphere is \(3 R / 8\) from the flat surface of the hemisphere (starting from point \(\mathrm{O}\) and perpendicular to the diameter \(\mathrm{AB})\). Determine:

1. the mass density of the sphere;

2. the magnitude of the horizontal force \(F\) that is responsible for the movement of the hemisphere;

3. the total torque \(\tau\) with respect to point \(\mathrm{O}\);

4. the inclination angle \(\theta\) of the hemisphere;

5. (briefly) explain why in this kind of situations the torque \(\tau\) does not depend on the choice of the pole;

6. Prove that the center of mass is at a distance of \(3 R / 8\) from the flat surface of the hemisphere.

 Fig. 7.16

For point (6): draw the inverted hemisphere, with diameter AB on the horizontal plane, and axiszz perpendicular and outward-facing from point 0; the radiusrr of the circumference in the plane parallel to AB at a height0 less than or equals z upper R 0 ≤ z ≤ R isr equals StartRoot left parenthesis upper R squared minus z right EndRoot r = (R2 − z2).

Transcribed Image Text:

C 0 B F