A primed frame moves at (V=(3 / 5) c) relative to an unprimed frame. Just as their
Question:
A primed frame moves at \(V=(3 / 5) c\) relative to an unprimed frame. Just as their origins pass, clocks at the origins of both frames read zero, and a flashbulb explodes at that point. Later, the flash is seen by observer \(A\) at rest in the primed frame, whose position is \(x^{\prime}, y^{\prime}, z^{\prime}=(3 \mathrm{~m}, 0,0)\).
(a) What does A's clock read when A sees the flash?
(b) When A sees the flash, where is she located according to unprimed observers?
(c) To unprimed observers, what do their own clocks read when A sees the flash? Use the Lorentz transformation of Eqs. 2.15.
Data from Eqs. 2.15
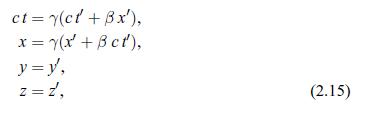
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





