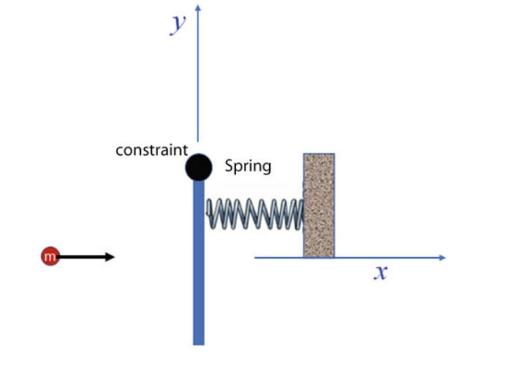
A rod of length \(D=150 \mathrm{~cm}\), mass \(M=150 \mathrm{~g}\) is constrained to rotate freely in the \(x y\) plane about one end, Fig. 13.8. At a distance of \(D / 5\) from the constraint, the rod is attached to a spring of elastic constant \(k=64 \mathrm{~N} / \mathrm{m}\), fixed in the plane at the other end; the spring is at rest when the rod is in the initial position, shown in the figure (top view). A point filler ball is thrown orthogonally to the rod and at time \(t=0\) hits it exactly in the center, sticking to it. The mass of the ball is \(m=0.025 \mathrm{~kg}\) and its speed is \(v=4 \mathrm{~m} / \mathrm{s}\). Determine:

1. the moment of inertia of the rod with respect to the constraint;

2. the angular speed \(\omega\) of the rod immediately after the impact of the ball. As a result of the impact and the presence of the spring, the rod begins to oscillate.

3. The period \(T\) of the small oscillations of the rod;

4. the maximum angle reached by the rod;

5. Draw the graph of the coordinate \(x\) of the ball as a function of time \(t\) in the time interval between \(t=-2 T\) and \(t=2 T\), where \(T\) is the period of the oscillations.

6. Note that following the collision, it appears that the linear momentum of the system is not conserved. This is related to the fact that the constraint exerts an impulsive force on the system. Determine what is the impulse provided by the constraint in the impact.

Fig. 13.8

Transcribed Image Text:

m y constraint Spring www X