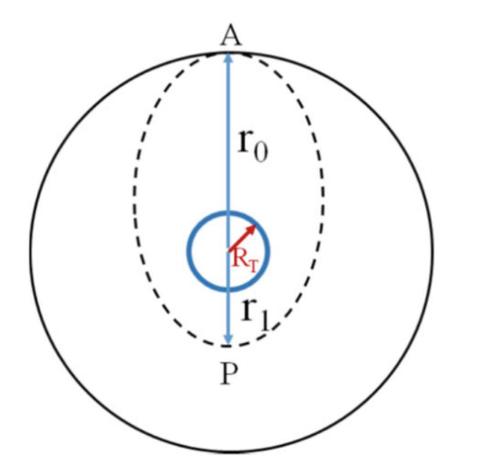
An artificial satellite is initially located at a point A at a distance \(r_{0}=4.0 \times 10^{4} \mathrm{~km}\) from the center of the Earth, as in Fig. 11.17. Neglecting any friction, calculate \(\left(G=6.67 \times 10^{-11}\right.\) \(\left.\mathrm{N} \mathrm{m}^{2} / \mathrm{kg}^{2}, M_{T}=5.97 \times 10^{24} \mathrm{~kg} ; R_{T}=6.37 \times 10^{3} \mathrm{~km}\right):\)

1. The speed with which it would reach the Earth's surface if it were left free at rest in a reference frame integral with the Earth;

2. the speed \(v_{0}\) that the satellite would have to have to travel a circular orbit of radius \(r_{0}\) around the Earth;

3. briefly discuss what would happen to the satellite if it were to increase the speed \(v_{0}\) at point \(\mathrm{A}\).

4. If, on the other hand, at A the satellite had velocity \(v_{A}=v_{0} / 2\) it would travel in an elliptical orbit, as shown in the figure. Determine the distance \(r_{1}\) of the second vertex \(\mathrm{P}\) of the orbit from the center of the Earth.

5. Determine the velocity at that point \(\mathrm{P}\).

Fig. 11.17

A To P