Consider the system shown in Fig. 6.8.. The spring has spring constant \(k=500\) \(\mathrm{N} / \mathrm{m}\) and rest length \(L_{0}=25.0 \mathrm{~cm}\). Initially a mass \(m=300 \mathrm{~g}\) compresses the spring, reducing its length to \(L=10.0 \mathrm{~cm}\). At the initial time \((t=0)\) the mass is allowed to move freely in the horizontal plane: it reaches the edge \(B\) and then falls to a plane below: \(h=\overline{O B}=75.0 \mathrm{~cm}\). There is friction between the mass and the horizontal plane, and the distance between the initial position of the mass and the edge \(B\) is \(d=2.20 \mathrm{~m}\). Knowing that the mass \(m\) reaches the edge \(B\) with speed \(v_{0}=3.00 \mathrm{~m} / \mathrm{s}\), determine:

1. the dynamic friction coefficient \(\mu_{d}\) between mass and horizontal plane;

2. the speed with which the mass arrives at the point \(P\);

3. the components of the velocity at \(P\);

4. the distance OP.

Fig. 6.8

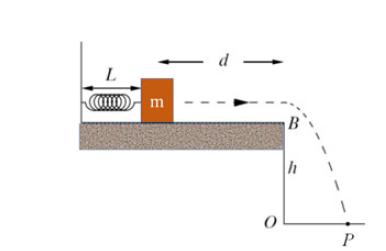
L m d 0 B h P